Datos necesarios para construir un polígono
Para construir un polígono en geometría se necesitan al menos tres datos esenciales.
1.- Construcción de un triángulo conociendo los tres lados:
Los datos son los lados a=BC, b=CA y c=AB. Se sitúa uno de los lados, por ejemplo el a=BC, y con centros en By C se trazan los arcos 1y 2, de radios c y b, respectivamente; estos arcos se cortan en el vértice A, que unido con B y C define el triángulo.
Construcción del triángulo conociendo los tres lados
2.- Construcción de un triángulo conociendo un lado y los ángulos adyacentes:
Los datos son el lado a=BC y los ángulos adyacentes B y C al lado a; en el vértice B se dibuja el ángulo de B con ayuda del arco 1-2 y en el vértice C se dibuja el ángulo de Cº con ayuda del ángulo 3-4; los lados c y b de estos ángulos, prolongados, se cortan en el vértice A, que completa el triángulo.
Construcción de un triángulo conociendo un lado y los ángulos adyacentes
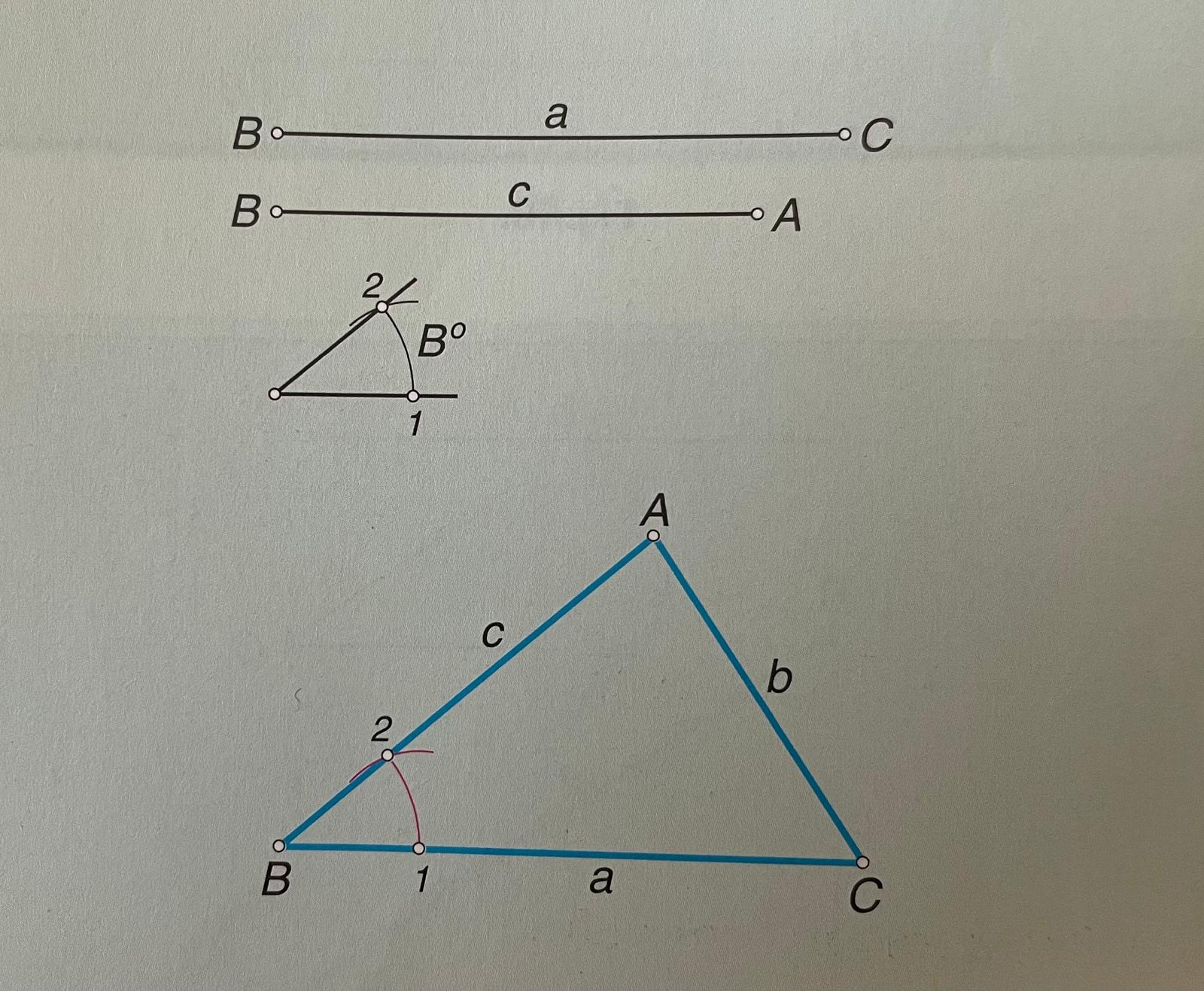
3.- Construcción de un triángulo conociendo dos lados y el ángulo comprendido:
Los datos son los lados a=BC y c=BA y el ángulo B; se coloca uno de los lados conocidos, por ejemplo; el a=BC, y en el vértice B se construye el ángulo de Bº con ayuda del arco 1-2; sobre el lado obtenido de este ángulo se lleva c=BA; finalmente se une A con C para completar el triángulo.
Construcción de un triángulo conociendo dos lados y el triángulo comprendido
4.- Construcción de un triángulo equilátero a partir del lado
El problema se resuelva como el de Construcción de un triángulo conociendo los tres lados, ya que realmente se conocen los tres lados, pues son iguales. Con centros en C y B y radio a se trazan dos arcos que se cortan en el tercer vértice A.
Triángulo equilátero dado el lado
5.- Construcción de un triángulo equilátero conocida su altura:
Como todos los triángulos equiláteros son semejantes, se construye uno cualquiera, por ejemplo: el 1-2-3, cuya altura resulta ser N-3; sobre N-3 prolongada se lleva a partir de N la altura h dada, con lo que se obtiene el vértice A; por paralelas se completa el triángulo.
Cada punto de una de ellas tiene su correspondiente en la otra y las líneas, que tienen la misma dirección relativa, están en la misma relación; esta relación es la razón de semejanza.
Semejanza en dibujo técnico
6.- Construcción de un triángulo rectángulo conociendo los dos catetos b y c:
Se sitúa uno de ellos, el c=AB, por el extremo A se traza la perpendicular, y después se lleva sobre ella el otro cateto b. Uniendo C con B se completa el triángulo.
Triángulo rectángulo conociendo dos catetos
7.- Construcción de un triángulo rectángulo conociendo un cateto b y un ángulo agudo C:
Se sitúa el lado b=AC en el vértice C se construye el ángulo C. Por A se traza la perpendicular al lado b hasta que corte en B al lado a del ángulo C.
Triángulo rectángulo conociendo un cateto y el ángulo agudo
8.- Construcción de un triángulo rectángulo dados un cateto y la hipotenusa:
Los datos son el cateto b y la hipotenusa a. En la parte superior de la figura se sitúa la hipotenusa a=BC y se traza la semicircunferencia de diámetro BC; desde C se corta con radio b a la circunferencia en el punto A, que es el vértice del ángulo recto.
Por la teoría del arco capaz, el triángulo A= 90º abarca el segmento BC, que es un diámetro, es decir, un ángulo central de 180º.
En la parte inferior de la figura se coloca el cateto b=AC; se traza la perpendicular a él por A y desde C se corta a dicha perpendicular con el arco 2 de radio a, con lo que se obtiene el vértice B.
Paso a paso de la construcción de un triángulo rectángulo dado un cateto y la hipotenusa
9.- Construcción de un triángulo isósceles conociendo uno de los lados iguales a y el ángulo desigual B:
Se sitúa el lado a y sobre un extremo, el B, se construye el ángulo dado B; después se lleva sobre el lado obtenido el lado a=c, finalmente se unen A y C.
Triángulo isósceles conociendo uno de los lados iguales y el ángulo desigual
10.- Construcción de un triángulo isósceles conociendo el lado desigual b y un ángulo igual A:
Triángulo isósceles conociendo el lado desigual b y un ángulo igual A
1.- Construcción de un triángulo isósceles conociendo uno de los lados iguales a y uno de los ángulos iguales C:
S toma el lado a=CB y se construye el ángulo C; desde el vértice B se corta al lado b con radio a y se tiene el tercer vértice A.











No hay comentarios:
Publicar un comentario