Tema 8: Curvas técnicas
Las curvas técnicas junto con las curvas cónicas forman parte de la familia de las curvas geométricas que son de gran utilidad tanto en la arquitectura como en la ingeniería.
De entre todas ellas, vamos a estudiar las curvas planas que se dibujan mediante la unión de arcos de circunferencias tangentes.
Dentro de este tipo de curvas podemos distinguir entre las cerradas, como el óvalo y el ovoide y las abiertas, que serían las espirales o volutas.
1.- Óvalo
Es una circunferencia plana y cerrada, simétrica respecto a sus dos ejes perpendiculares y formada por cuatro arcos de circunferencia iguales dos a dos.
1.1.- Óvalo conociendo el eje menor
1.- Colocas el eje menor dado en posición vertical. Haces la mediatriz del segmento, conseguimos el punto O.
2.- Desde O y con radio OC hacemos una circunferencia, que corta con el eje mayor en los puntos O1 y O2.
3.- Unimos C y D con O1 y O2 alargando las líneas.
4.- Desde C y D respectivamente y con radio CD se trazan dos arcos que cortan en la prolongación de las líneas C y D y O1 y O2. Surgen así los puntos P y P' y Q y Q'.
5.- Con centro en O1 y radio O1P, y con centro en O2 y radio O2P' se trazan los otros dos arcos para unir P con Q, y P' con Q'.
Paso a paso óvalo dado el eje menor
1.2.- Óvalo conociendo el eje mayor (primer procedimiento)
1.- Se divide el eje mayor en tres partes iguales. Surgen los puntos O y O'.
2.- Con centro en O y O' y radio OA y O'B se trazan dos circunferencias, donde cortan ambas circunferencias surgen los puntos O2 y O3.
3.- Se unen los cuatro centros prolongando la recta por O y O1. Surgen los puntos P y P' y Q y Q'.
4.- Desde O2 y O3 y con radio O2Q y O3P trazamos dos arcos que determinan el óvalo.
Óvalo dado el eje mayor (primer procedimiento)
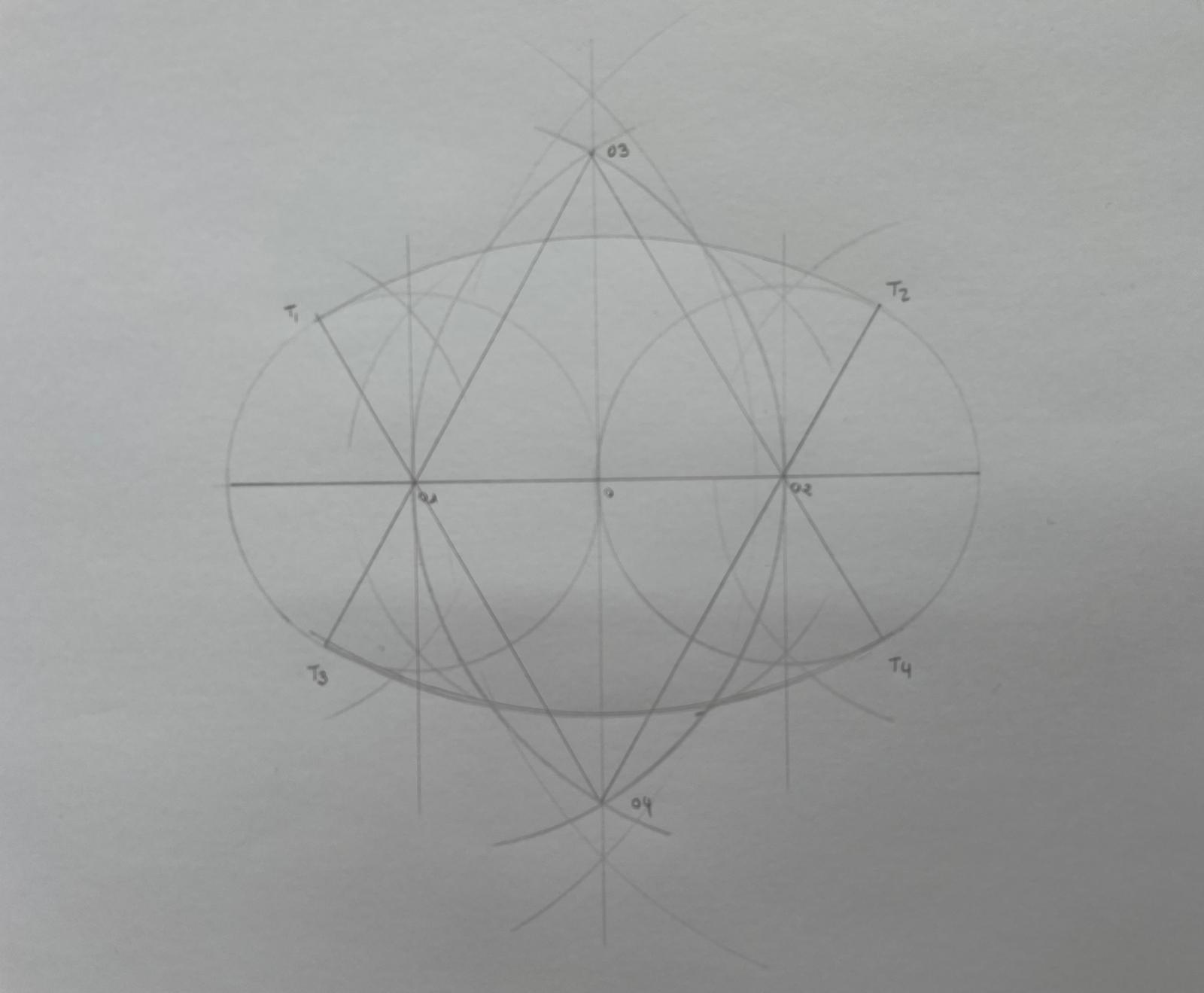
1.3.- Óvalo conociendo el eje mayor (segundo procedimiento)
1.- Trazamos la mediatriz del eje AB obteniendo O. Trazamos mediatrices a los dos semi-ejes obteniendo O1 y O2.
2.- Trazamos dos circunferencias desde O1 y O2 abriendo el compás hasta O. Desde O1 y O2 trazamos dos arcos abriendo el compás desde O1 hasta O2 y desde O2 hasta O1 hasta que corten esos puntos con la mediatriz del segmento surgiendo así los puntos O3 y O4.
3.- Unimos los centros para conseguir los puntos de tangencia. Después desde los centros O3 y O4 se realizan los arcos que completan el óvalo.
Óvalo conociendo el eje mayor (segundo procedimiento)
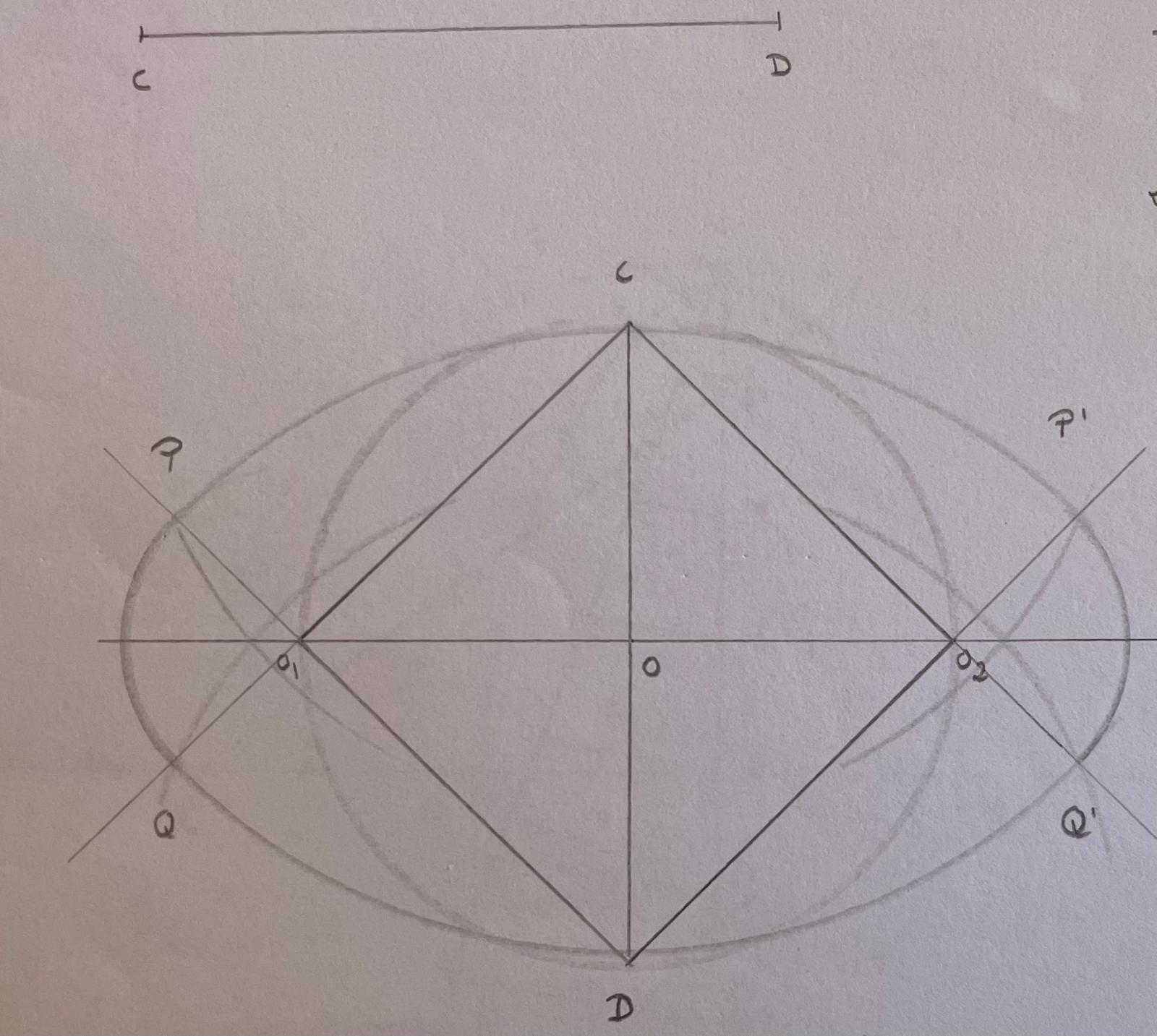
1.4.- Óvalo conociendo los dos ejes
1.- Colocas el eje mayor AB dado. Realizas la mediatriz para situar el segundo eje CD (el eje menor). De la mediatriz surge el punto O.
2.- Haciendo la mediatriz del eje menor (punto M) sabemos qué distancia exacta debemos poner en la mediatriz del eje mayor (punto O), transportando con dicho compás la medida exacta. Surgiendo así los puntos C y D.
3.- Con centro en O y radio OA voy hacer un arco de circunferencia que va a cortar a la prolongación de la mediatriz por encima del punto C. Surgiendo el punto A'.
4.- El siguiente paso es unir los puntos AC. Con centro en C y radio CA' voy a hacer un arco que cortará con la unión que AC en un punto llamado A''.
5.- Después realizaremos la mediatriz del segmento A y A''. Esta mediatriz va a cortar en los dos ejes (eje mayor y eje menor) en los puntos O1 y O2. Estos puntos van a ser centros de los óvalos que buscamos.
6.- A continuación voy a buscar sus simétricos, es decir, simétrico de O1 respecto al eje CD va a estar otro centro (O3) y simétrico de O2 respecto al eje AB, ahí vamos a encontrar el cuarto centro (O4).
7.- A continuación unimos de O2 a O3 y prolongamos, de O4 a O1 y prolongamos y de O4 a O3 y prolongamos también. Ya solo queda dibujar los arcos de circunferencia que van a conformar el óvalo que busco. De O1 y radio hasta A dibujo el primer arco hasta las prolongaciones, con ese mismo radio y centro en O3 voy a dibujar otro tramo también hasta las prolongaciones. Cogiendo el centro en O2 hacemos el siguiente arco desde la prolongación y por último con centro en O4 y realizamos el arco que falta hasta la prolongación.
2.- Ovoide
El ovoide es una curva plana y cerrada, simétrica solo respecto a su eje mayor y formada por cuatro arcos de circunferencia, de los que dos son iguales y los otros dos son diferentes.
2.1.- Ovoide conociendo el eje mayor
1.- Dividir el eje mayor AB en 6 partes iguales.
2.- Perpendicular a AB que pase por el punto 2.
3.- Centro en 2 y radio 2A y trazo un arco que corta con la perpendicular. Surgen los puntos C y D.
4.- Desde estos puntos C y D trazo líneas que pasen por el punto 5. Donde cortan con el arco surgen los puntos P y P'
5.- Desde el punto 2 y con radio 2B trazamos un arco. Surgen los puntos Q y Q'.
6.- Desde C y D respectivamente y con radio a los puntos Q y Q' se traza un arco que corta con los puntos P y P'.
7.- Desde el punto 5 y con radio 5-6 trazamos el arco que nos falta.
Ovoide conociendo el eje mayor
Paso a paso de un ovoide dado el eje mayor
2.2.- Ovoide conociendo el eje menor
1.- Mediatriz del segmento AB y conseguimos el punto O.
2.- Desde O y radio OA trazamos una circunferencia y encontramos el punto P
3.- Unimos A con B con P y prolongamos sus lados.
4.- Desde A y B respectivamente y con radio AB trazamos arcos que corten con los puntos M y M'.
5.- Desde P y con radio PM trazamos el último arco.
2.3.- Ovoide conociendo los dos ejes
1.- El primer paso va a ser situar en una vertical el eje CD. Calculamos la mediatriz y la prolongamos el punto medio del segmento CD recibirá el nombre de O.
2.- Vamos a hacer una circunferencia con centro en O (mediatriz) y radio OD, obtenemos dos puntos que les vamos a llamar B y E. Con la medida AB vamos a colocar el eje mayor, cogemos la medida con el compás y nos colocamos en el punto B y donde corta en la prolongación de la mediatriz hayamos el punto A.
3.- Ahora vamos a hacer centro en E y radio EA y realizamos una circunferencia. Con esta misma medida vamos a uno de los extremos y centro en D hacemos una marca en el eje menor surgiendo así el punto F.
4.- A continuación unimos el punto F con el punto E. Hacemos la mediatriz de la unión de F y E. Prolongamos la mediatriz hasta que corte con la prolongación del eje menor. A este punto lo podemos llamar G.
5.- Haciendo centro en O y con radio OG transportamos la medida al otro lado del eje y conseguimos el punto H. Trazamos una recta desde H hasta E y prolongamos hasta cortar la circunferencia con A surge el punto I y unimos G con E hasta cortar la circunferencia con A y de aquí surge el punto J.
6.- Ya tenemos todos los puntos de enlace siendo G y H los últimos centros que enlazan ambas circunferencias.
3.- La espiral
La espiral es una línea curva generada por un punto que se va alejando progresivamente de otro punto a la vez que gira alrededor de él. La curva generada es complicada de trazar, pues no se puede resolver por arcos de circunferencia. Se suele trazar bien a mano alzada, bien con una plantilla de curvas.
3.1.- Espiral de tres centros (base triangular)
Partimos de un triángulo equilátero cuyo lado mide un tercio del paso.
1.- Prolongamos las líneas del triángulo. Cada vértice del triángulo lo vamos a numerar 1, 2 y 3.
2.- Con centro en 1 y radio 1-2 vamos a trazar un arco hasta llegar a la prolongación del punto 1.
3.- Con centro en 2 ajustamos hasta el corte de la prolongación de 1 y hacemos un arco que corta con la prolongación de 2.
4.- Con centro en 3 ajustamos hasta el corte de la prolongación de 2 y hacemos un arco que corta con la prolongación de 3.
5.- Otra vez con centro en 1 ajustamos hasta el corte de la prolongación de 3 y hacemos un arco que corta con la prolongación de 1. Y así sucesivamente se repite el mismo procedimiento.
3.2.- Otras espirales
Espiral de 4 centros (Base cuadrada)
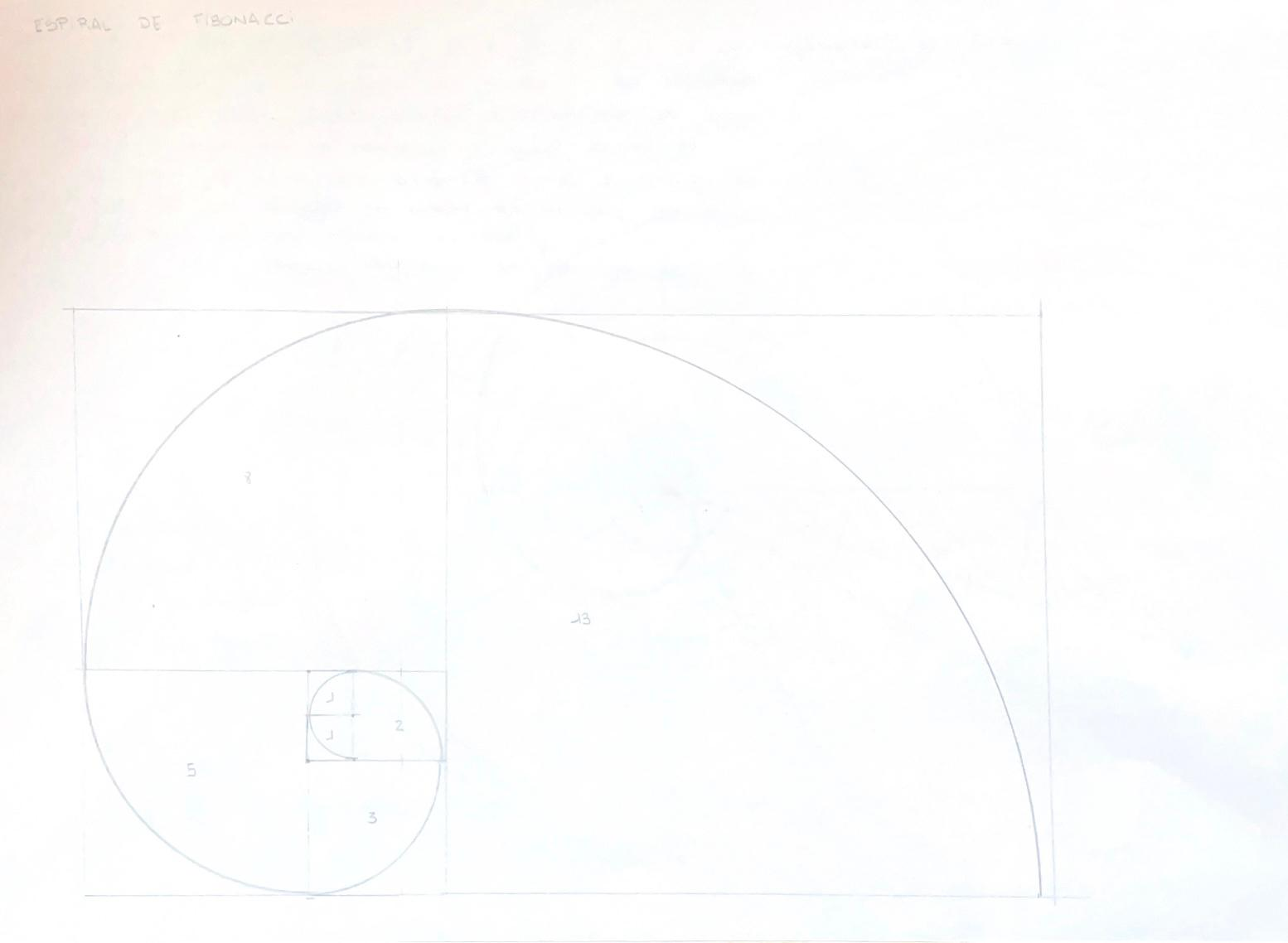
3.3.- Espiral de Fibonacci
La Espiral de Fibonacci (Sucesión de Fibonacci). La sucesión de Fibonacci es un número muy importante en matemáticas (0 1 1 2 3 5 8 13 21 34 55 89 144...). Partiendo del 0 y del 1 los demás números se van obteniendo como suma de los anteriores (0+1=1, 1+1=2, 2+3=5, etc.). Se confunde con la espiral áurea porque si dividimos un número entre su anterior esta división se va a ir aproximando cada vez más al número áureo. La proporción en la espiral de Fibonacci va a empezar siendo dos a uno y van a acabar poco a poco aproximándose cada vez más al rectángulo áureo.
1.- espiral de Fibonacci se empieza a hacer construyendo un cuadrado de 1 cm. Posteriormente se realiza otro cuadrado de un centímetro justo arriba del ya realizado. Posteriormente al lado se realiza un cuadrado de 2 cm. Abajo de estos 3 cuadrados construimos un cuadrado de 3 cm. En la parte izquierda de estos construimos uno de 5 cm. Sucesivamente arriba construimos uno de 8 cm. Al lado de todos estos construimos uno de 13 que va a ser el último porque más ya no caben en el formato A4. Si tuviéramos espacio podríamos continuar con el de 21, 34, etc.
2.- Empezamos haciendo arco entre los cuadrados de 1 cm. Posteriormente continuamos realizando los arcos (puntos rojos en el dibujo). Siempre seguimos el principio de las tangencias que nos obliga a que los centros de circunferencias tangentes están alineados con el punto de tangencia esto nos ayuda a encontrar los centros.
Espiral de Fibonacci paso a paso
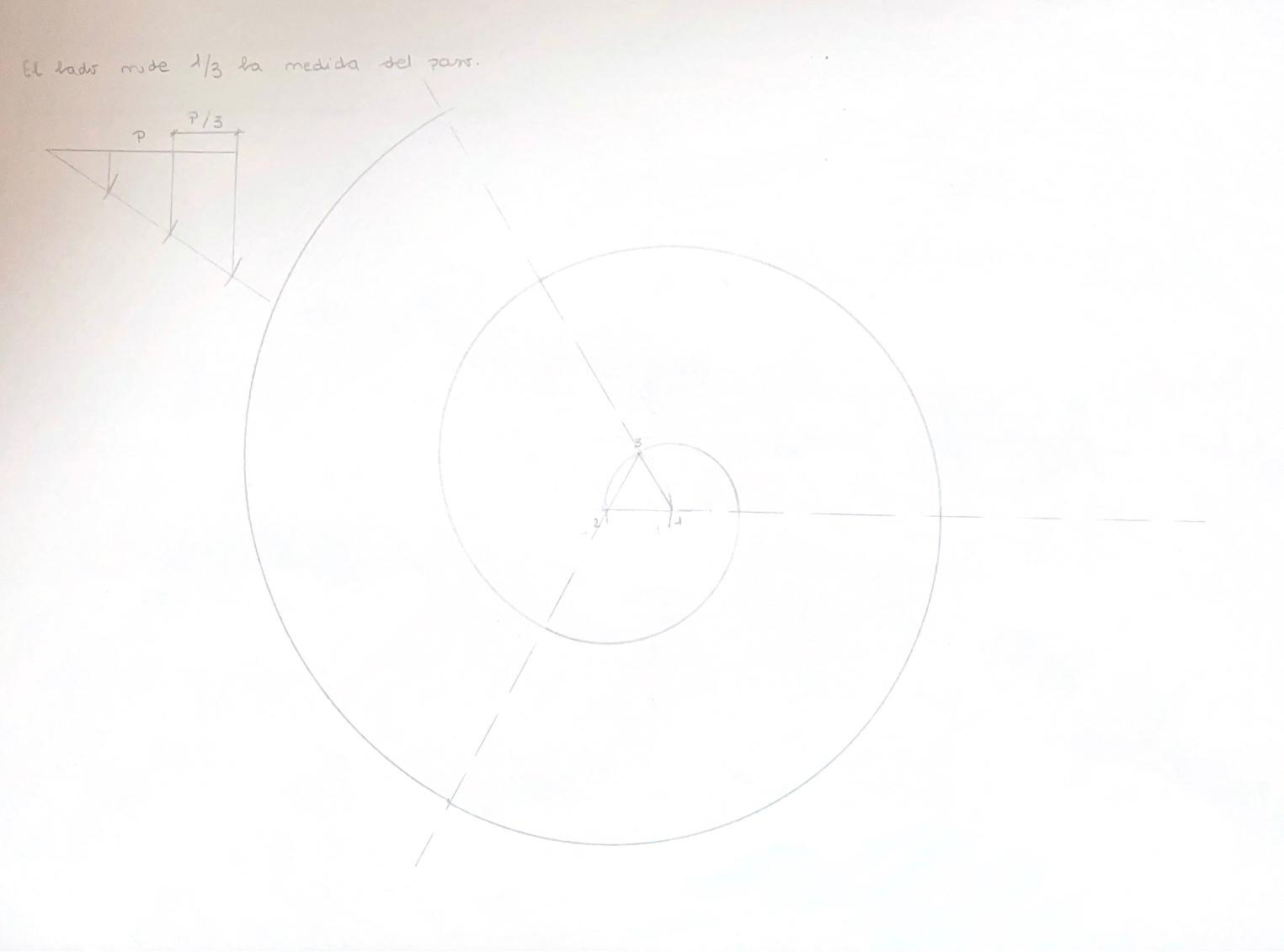
3.4.- Espiral de Arquímedes dado el paso
La Espiral de Arquímedes es la trayectoria o curva que describe un punto que se desplaza sobre una recta y al mismo tiempo esta recta gira a un punto alrededor de ella. Cada vuelta de la curva se denomina espira y a la distancia radial entre el principio y el fin de una espira la vamos a llamar paso.
Te dan el paso (distancia entre dos vueltas o espiras consecutivas). Si te dan el radio de la circunferencia, éste va a ser igual al paso.
1.- Realizas una recta auxiliar y sitúas un punto O en ella. A partir de O sitúas el paso dado surge el punto 1. Con centro en O y radio O1 realizo una circunferencia.
2.- Desde O realizo el Teorema de Thales y divido el segmento en 8 partes por ejemplo. La octava parte la uno con el punto 1. Realizamos el diámetro vertical de la circunferencia. Dividimos cada cuarto de la circunferencia en dos lados iguales (esto se consigue desde los diámetros de la circunferencia con la distancia del radio).
3.- Con centro en O y radio cada división del Teorema de Thales realizamos una circunferencia. En este caso en total 8.
4.- Situamos los puntos de la espiral que coincidirán con los diámetros y las circunferencias. Posteriormente unimos todos los arcos desde el centro hasta el punto 1.
Espiral de Arquímedes paso a paso






No hay comentarios:
Publicar un comentario