TEMA 3.1. RECTAS Y PUNTOS NOTABLES DE UN TRIÁNGULO
Presentación de Rectas y puntos notables de un triángulo Rectas y puntos notables de un triángulo
Vídeo de Rectas y puntos notables de un triángulo Rectas y puntos notables de un triángulo
Presentación
Vamos a ver una serie de rectas y sus intersecciones relacionadas con los lados, los ángulos y los vértices de un triángulo. Estas rectas y los puntos de intersección se denominan: rectas y puntos notables del triángulo y van a aparecer en multitud de problemas y aplicaciones de la geometría.
MEDIATRIZ - CIRCUNCENTRO
Se realiza la mediatriz de los lados del triángulo. (Una mediatriz es una recta perpendicular a un segmento en su punto medio).
La propiedad que se cumple es que la mediatriz es el lugar geométrico de los puntos del plano que equidista (está a la misma distancia) de los dos lados del segmento. El punto O por estar en las tres mediatrices a la vez va a estar a la misma distancia de los tres ejes del triángulo. Tiene la característica que si pinchamos en él y hacemos centro en los vértices la circunferencia va a pasar por los tres vértices del triángulo.
Si el triángulo es obtusángulo, es decir tiene un ángulo mayor a 90º, el circuncentro puede estar fuera del triángulo.
BISECTRIZ - INCENTRO
Las siguientes rectas notables que vamos a ver van a ser las bisectrices, que como ya sabéis se refieren a los ángulos del triángulo.
El punto de intersección de las tres bisectrices se denomina incentro del triángulo. Vamos a llamarlo con la letra I.
La propiedad que se cumple es que es el único punto del plano (triángulo) que está a la misma distancia de los tres lados del triángulo. Si hago centro en I y radio a la distancia de los lados obtendré una circunferencia que va a ser tangente a los tres lados. Circunferencia inscrita en el triángulo.
El punto de intersección de las tres bisectrices se denomina INCENTRO. Este punto siempre va a estar dentro
del triángulo.
Hay otros tres puntos que nos van a permitir trazar circunferencias tangentes a los tres lados. Si prolongamos los lados, el centro de esta circunferencia exterior se denomina exincentro y se calcula haciendo bisectrices a cada lado. Para hallar los puntos de tangencia hacemos perpendiculares a los lados que pasen por el exincentro.
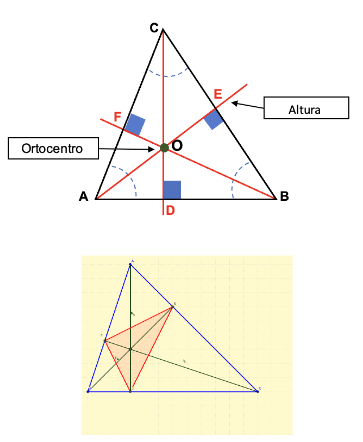
Las alturas son rectas que van desde cada uno de los vértices del triángulo perpendiculares al lado opuesto.
Cogemos la escuadra y el cartabón y la altura del lado AB sería la recta perpendicular desde el vértice C hasta
el lado AB. Hacemos lo mismo con los otros dos lados o vértices.
Las tres alturas se tienen que cortar en un punto que se denomina ORTOCENTRO del triángulo vamos a denominarlo con la letra H mayúscula. Si unimos los pies de las alturas se va a obtener otro triángulo que se va
a denominar triángulo órtico.
En los triángulos obtusángulos (con un ángulo mayor a 90º) el ortocentro va a estar fuera del triángulo.
MEDIANAS - CENTRO DE GRAVEDAD
Una mediana es una recta que va desde cada vértice del triángulo hasta el punto medio del lado opuesto. Hay que hacer una mediatriz de cada lado y el punto medio de la mediatriz se une con el vértice opuesto.
Las medianas van a intersecar en un punto llamado BARICENTRO o centro de gravedad de un triángulo. Lo llamamos con la letra G (centro de gravedad). También se le puede llamar con la letra B de Baricentro.
Toda la longitud de la mediana ⅔ partes están desde el vértice hasta el centro de gravedad.
El circuncentro, el baricentro y el ortocentro de un triángulo están alineados. La recta que pasa por ellos se denomina RECTA DE EULER.
Además la distancia entre el circuncentro y el baricentro es la mitad que la distancia entre el baricentro y el ortocentro.
Esto tiene sentido en todos los triángulos menos en los triángulos equiláteros porque en ellos va a coincidir tanto el circuncentro, como el baricentro, como el ortocentro además del incentro. En el triángulo equilátero no se puede hablar de la Recta de Euler.



No hay comentarios:
Publicar un comentario