TEMA 4.1.- CONSTRUCCIÓN DE CUADRILÁTEROS
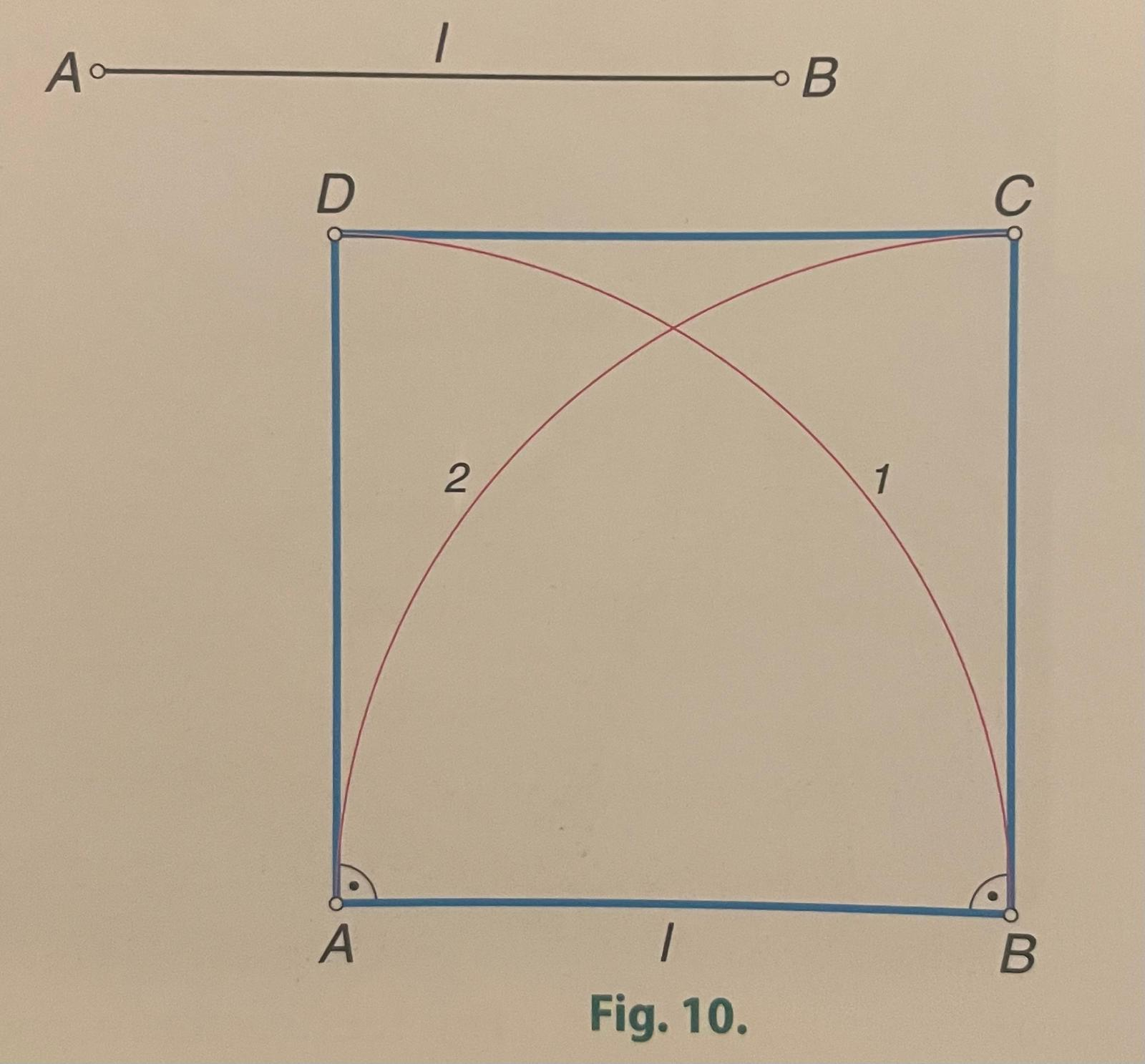
1.- Construcción del cuadrado a partir del lado.
Se coloca el lado AB; se trazan por A y B las perpendiculares a este lado y sobre ellas se lleva el lado por medio de los arcos 1 y 2; se obtienen así los vértices C y D que completan el cuadrado.
2.- Construcción de un cuadrado dada la diagonal.
Se toma la diagonal d = AC y sobre su mediatriz m se lleva, a partir de O y en los dos sentidos, la semidiagonal; de esta forma se tienen los dos vértices B y C. En la figura se ha dibujado la circunferencia circunscrita.
Construcción de un cuadrado dada su diagonal
3.- Construcción de un rectángulo conocidos sus lados.
Los datos son los lados a=AB y b=AC. Se sitúa AB y por A se traza la perpendicular a AB, problema ya conocido; sobre esta perpendicular se lleva el lado b= AC, con lo que se obtiene el vértice C; finalmente, por paralelas trazadas por los vértices B y C se completa el rectángulo.
Construcción de un rectángulo conocidos sus lados
4.- Construcción de un rectángulo conocidos una diagonal y un lado.
Se toma la diagona d=AC y con centro en su punto medio O se traza la circunferencia de radio OA=OC. Con centro en C se corta a la circunferencia con el radio a y se tiene el vértice B, el cual se une con A; por paralelas se completa el rectángulo ABCD.
Construcción de un rectángulo conocidos una diagonal y un lado
5- Construcción de un rombo dadas las dos diagonales.
Los datos son d=AC y d'=BD. Se dibuja AC y sobre la mediatriz de AC se lleva a partir de O la semidiagonal d'/2 en los dos sentidos: OB =OD =d'/2; uniendo los vértices se obtiene el rombo ABCD.
Construcción de un rombo dadas las dos diagonales
6.- Construcción de un rombo dados un lado y un ángulo.
A partir del lado a=AB se construye el ángulo A y se lleva sobre el lado obtenido el segmento a, con ayuda del arco 2. Por B y D se trazan paralelas a los lados AD y AB y se obtiene el vértice C.
Construcción de un rombo dados un lado y un ángulo
7.-Construcción de un trapecio isósceles dadas las bases y la altura.
Se conocen las bases b=AB y b'= CD y la altura h=NM. Se dibuja b=AB y se traza la mediatriz de AB; sobre ella se toma el segmento h=NM y por el extremo M se traza la paralela a AB; a partir de M y sobre la paralela trazada se lleva MC=MD=b'/2, con lo que se obtienen los vértices C y D que completan el trapecio ABCD.
Construcción de un trapecio isósceles dadas las bases y la altura
8.- Construcción de un trapecio rectángulo dadas las bases y la altura.
Se dan las bases b=AB y b'=CD y la altura h=AC. Se dibuja la base mayor AB y por un extremo, el A, se traza la perpendicular a ella, sobre la cual se lleva la altura AC; por C se dibuja la paralela AB y sobre ella se lleva la base menor b'=CD; al unir D con B se completa el polígono.
Construcción de un trapecio rectángulo dadas las bases y la altura
9.- Construcción de un romboide dados sus lados y el ángulo que los forman.
Se conocen los lados a=AB y b=AD y el ángulo A que forman. Se toma a=AB y se construye el ángulo A con ayuda del arco 1-2; sobre el lado obtenido de éste ángulo se toma b=AD; finalmente, por paralelas a los lados por los vértices B y D se completa el romboide ABCD.
Construcción de un romboide dados sus lados y el ángulo que los forman
En este tema se resuelven dos tipos de ejercicios:
- Dividir una circunferencia en un número cualquiera de partes iguales, o, lo que es igual, inscribir polígonos regulares en una circunferencia, pues para ello basta unir los puntos de división obtenidos.
- Construir un polígono regular de cualquier número de lados a partir del lado conocido.
10.- División de una circunferencia en tres y seis partes iguales.
Para dividir en seis partes, es decir, para constituir el hexágono regular inscrito en una circunferencia, basta tomar el radio R e ir llevando cuerdas consecutivas; uniendo los puntos de división A,B,C,D,E y F se tiene el hexágono; si se unen de dos en dos los puntos obtenidos, se obtiene el triángulo equilátero inscrito. Trazando las bisectrices de los ángulos centrales se pueden obtener 12, 24, 48, etc.; partes iguales.
División de una circunferencia en tres partes iguales
División de una circunferencia en 6 partes iguales
11.- División de la circunferencia en cuatro y en ocho partes iguales.
Para dividir la circunferencia en cuatro partes iguales, basta trazar una pareja de diámetros perpendiculares AE y CG; uniendo los extremos se obtiene el cuadrado ACEG. Dibujando la bisectriz del ángulo central AOG se tiene el punto H, medio del arco AG; El segmento AH=HG es el lado del octógono regular inscrito. Trazando nuevas bisectrices de los ángulos centrales, se pueden obtener 16,32, 64, etc; partes iguales.
División de una circunferencia en cuatro partes iguales
División de una circunferencia en ocho partes iguales
12.- División de la circunferencia en cinco y en diez partes iguales.
Se trazan dos diámetros perpendiculares, con centro en M y radio MO se traza el arco ON; la perpendicular por N a OM da el punto medio L a OM; con centro en L y radio LA, se traza el arco AP; el segmento AP es el lado l5 del pentágono inscrito, por lo que basta tomar la cuerda l5 cinco veces para obtener el polígono. Esta construcción puede aprovecharse para construir el decágono, ya que el OP es el lado l10 del polígono de diez lados.
Para el decágono se puede utilizar otro procedimiento, que se indica en la siguiente figura. Se trazan dos diámetros perpendiculares AF y PL; con centro en N, punto medio OL, se traza la circunferencia de radio NO=NL. Uniendo A y N se obtiene el punto M en esta circunferencia; el segmento AM es el lado del decágono.
División de la circunferencia en 5 partes iguales
División de la circunferencia en 10 partes iguales
13.- División de la circunferencia en siete partes iguales.
Se halla el punto medio P del radio ON, para lo cual se traza el arco OQ de centro N y desde Q se traza la perpendicular a ON. El segmento PQ es el lado l7 del heptágono inscrito en la circunferencia; se lleva siete veces AB=PQ y se obtiene el polígono.
División de una circunferencia en 7 partes iguales
14.- División de la circunferencia en nueve partes iguales.
Se dibujan dos diámetros perpendiculares, AN y PR; con centros en A y N se trazan los arcos 0-2 y 0-1, respectivamente; con centros en A y en N se trazan los arcos 1-3 y 2-3, los cuales se cortan en el punto 3, en la prolongación de PR; con centro en 3 se traza el arco AQN y el segmento PQ es el lado del eneágono inscrito en la circunferencia, que se lleva nueve veces sobre ella.
División de la circunferencia en nueve partes iguales
15.- División de la circunferencia en un número n cualquiera de partes iguales.
Se trazan dos diámetros perpendiculares AB y CD, y se divide uno de ellos, CD, en tantas partes iguales como se desee dividir la circunferencia, en este caso, once partes; con centros en C y D se trazan los arcos DE y CE, que se cortan en E, y este punto se une con la división 2 del diámetro; al prolongar la recta E-2 se obtiene el punto F en la circunferencia. El segmento CF=l11, es el lado del polígono regular de once lados inscritos en dicha circunferencia.
Método general para dividir una circunferencia en partes iguales
Esta construcción sirve para solucionar todos los problemas que se presenten en la división de la circunferencia en un número cualquiera de partes iguales.
116
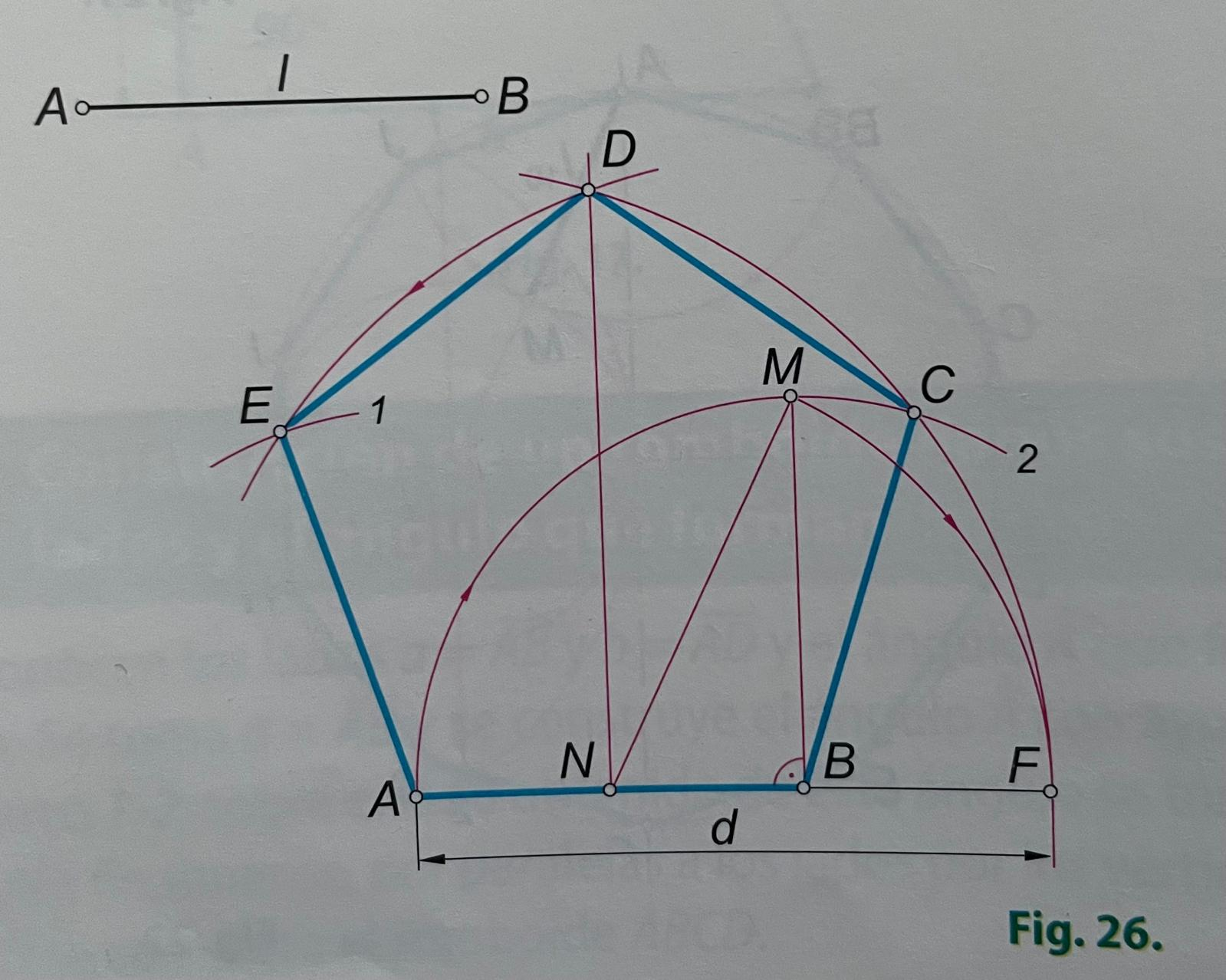
16.- Construcción del pentágono regular a partir del lado.
El lado conocido es l=AB. Se toma AB y se traza la mediatriz de AB; se toma BM=BA con ayuda del arco 2; con centro en N y radio NM se traza el arco MF; el segmento AF es la diagonal d del pentágono que se busca; con radio d y centros en A y B se trazan dos arcos que en D; con centro en A y radio l=AB se traza el arco 1, que corta en E el arco DE de centro en B; de la misma forma se obtiene el punto C, último vértice del pentágono.
Construcción de un pentágono regular dado el lado
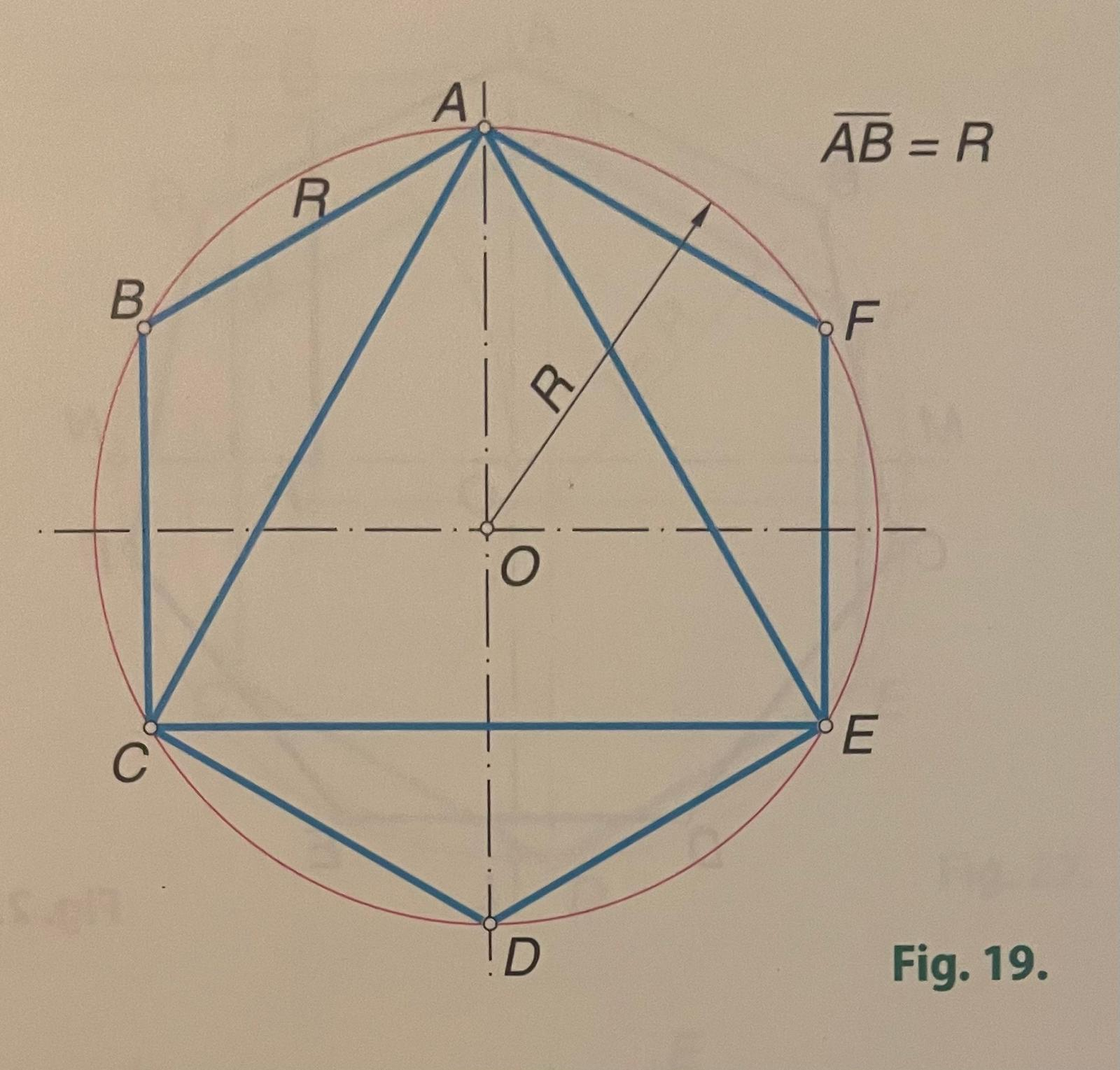
17.- Construcción del hexágono regular a partir del lado.
El lado conocido es l. Se construye la circunferencia de radio R=l y se inscribe en ella el hexágono. El lado de un hexágono es igual al radio de la circunferencia circunscrita a él.
Construcción de un hexágono regular dado el lado
18.- Construcción del heptágono regular a partir del lado.
El lado l=AB. Se traza la mediatriz m de AB y se dibujan los arcos AN y BN con centros en B y A, respectivamente; se traza la bisectriz del ángulo NAB, la cual corta en M a la perpendicular a AB en el punto B; con centro en A y radio AM, se traza el arco MO y el punto O de la mediatriz es el centro de la circunferencia circunscrita al polígono; sobre esta circunferencia se lleva siete veces el lado AB y se obtiene el heptágono.
Construcción de un heptágono regular dado el lado
19.- Construcción del octógono regular a partir del lado.
Se coloca el lado l8=AB se traza su mediatriz m; con el segmento AB como lado, se construye el cuadrado ABCD; se traza la circunferencia circunscrita al citado cuadrado, la cual corta en el punto O y radio OA se dibuja la circunferencia en la que está inscrito el octógono; sobre esta circunferencia se lleva ocho veces el lado AB.
Construcción de un octógono regular dado el lado
20.- Construcción del eneágono regular a partir del lado.
Se dibuja el lado conocido AB=l9; se traza la mediatriz de AB y se construye el triángulo equilátero ABM; se dibuja la bisectriz del ángulo MAB y se tiene el punto N en la mediatriz; con centro en M y radio MN se dibuja la circunferencia que corta en P y Q a las prolongaciones de los lados BM y AM; uniendo P con Q se obtiene el punto O en la mediatriz; este punto O es el centro de la circunferencia circunscrita al polígono, sobre la que se lleva nueve veces el lado AB.
Construcción de un eneágono regular dado el lado
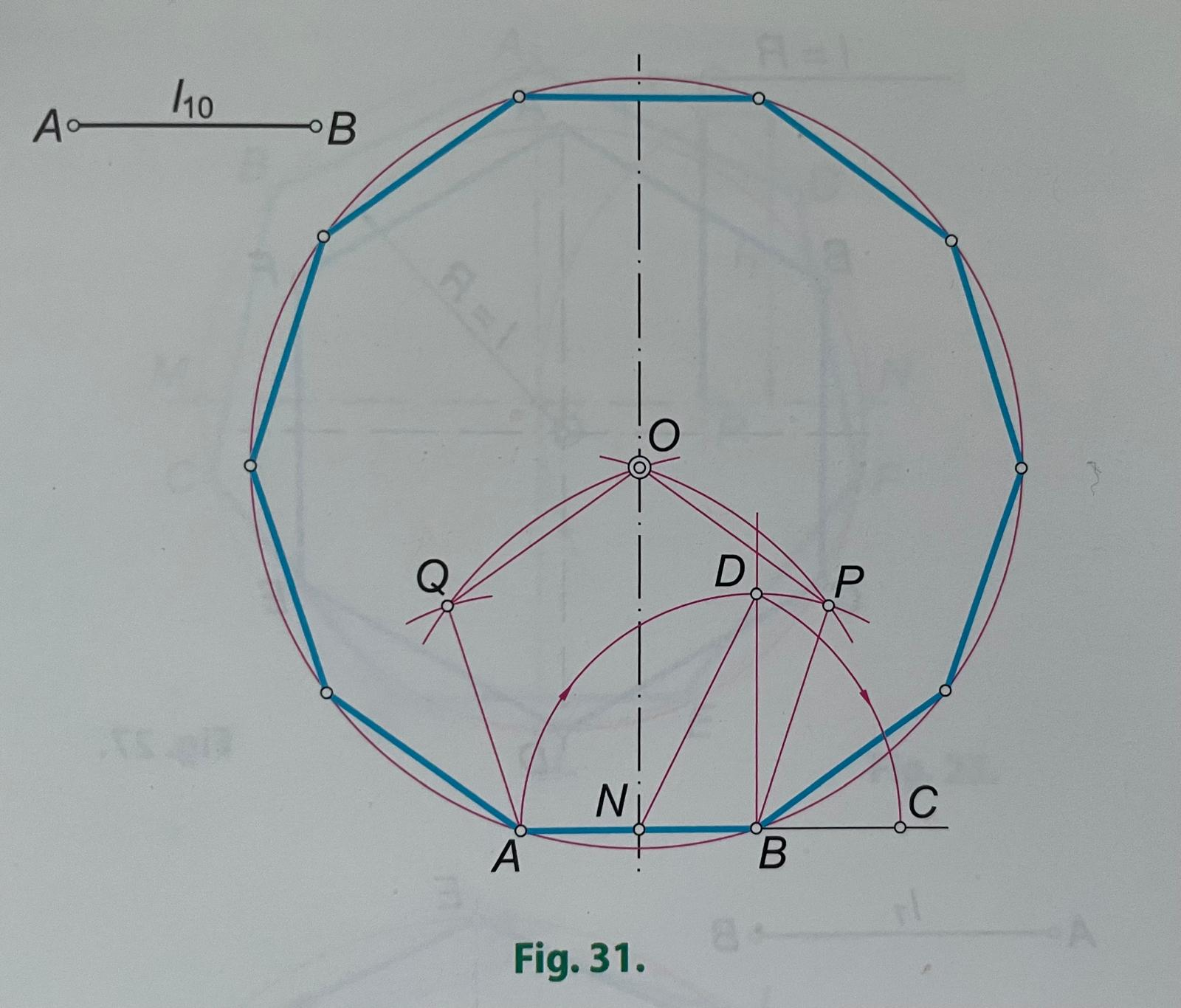
21.- Construcción del decágono regular a partir del lado.
A partir del lado AB=l10 conocido, se construye, como ya se ha visto, el pentágono regular ABPOQ; el vértice O de este polígono es el centro de la circunferencia circunscrita al decágono; por ello, con centro O y radio OA=OB, se traza la circunferencia y se lleva sobre ella el lado AB diez veces.
Construcción decágono regular dado el lado
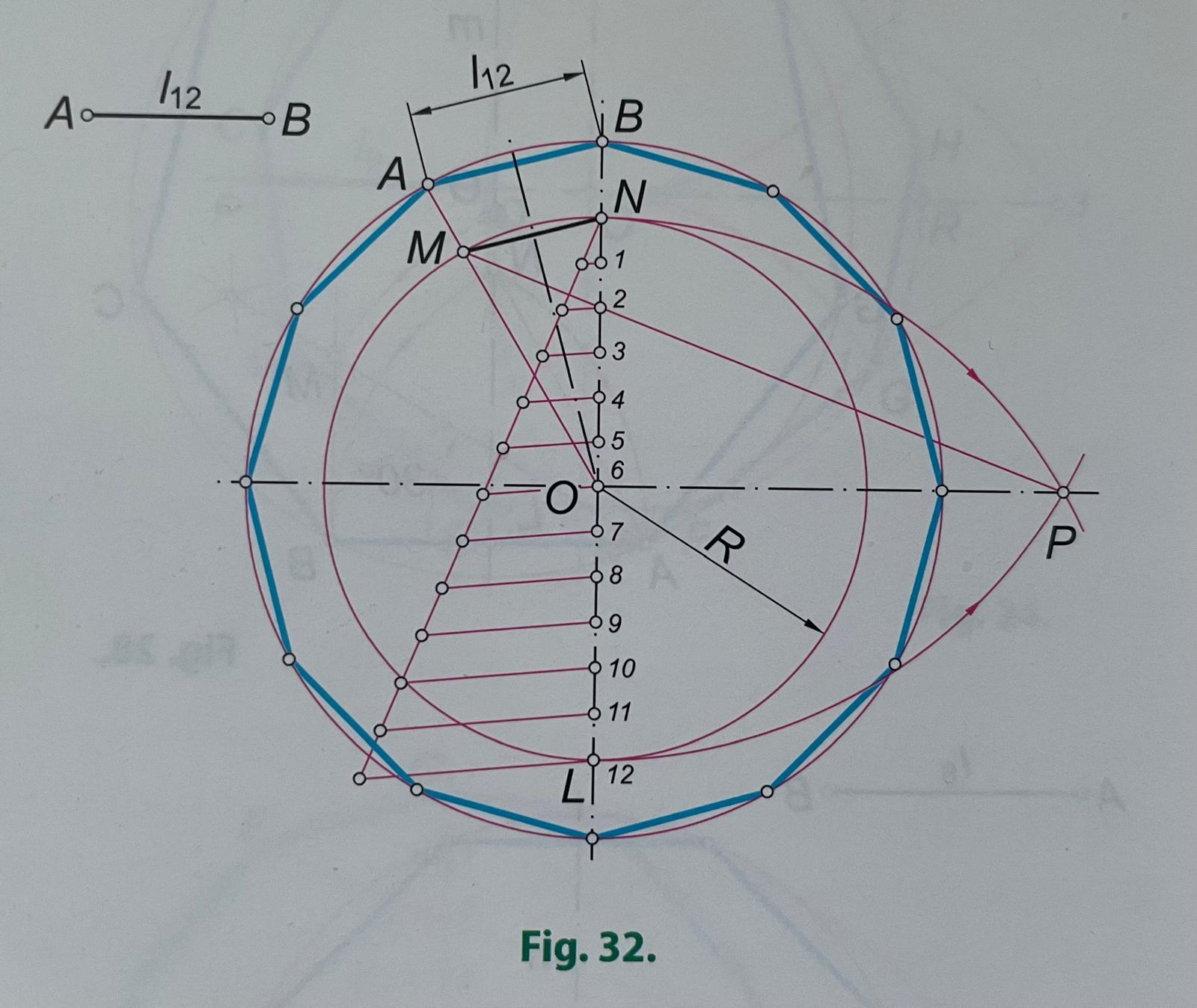
22.- Construcción de un polígono regular de n lados a partir del lado.
Se supone que el polígono ha de tener n=12 lados, siendo el lado l12 lados, , siendo el lado l12=AB. Por el procedimiento general ya visto, se divide una circunferencia cualquiera en doce partes iguales; en la figura se ha obtenido el lado N-M. Como el dato es AB, se inscribe este segmento AB en el ángulo central NOM del dodecágono paralelo y paralelo a NM. Con centro en O y radio OA=OB se traza la circunferencia en la que está inscrito el polígono.
En la figura de abajo se inscribe de otra forma el lado AB en el ángulo central NOM. Se toma AB sobre NM, a partir de N, NT=AB y por T se traza la paralela del diámetro NL, la cual corta a la prolongación del radio OM en A.
Finalmente, un polígono regular de n lados se puede construir con el transportador de ángulos, fijando el ángulo central que corresponde a un lado; este ángulo central valdrá 360º/n.
Método general para construir polígonos dado el lado
23.- Polígonos regulares estrellados:
Los polígonos estrellados son polígonos regulares cóncavos cruzados con forma de estrella. Se obtienen de unir de forma alterna, de dos en dos, de tres en tres..., los vértices de un polígono regular convexo.
No se pueden obtener polígonos estrellados de todos los polígonos. Y en algunos casos podremos obtener más de un polígono estrellado de un mismo polígono.
Propiedades de un polígono estrellado
Estas son las propiedades de un polígono estrellado:
- Género: Es el número de lados que forman el polígono.
- Especie: Es el número de vueltas que debemos dar antes de completar la figura.
- Paso: Es el número de divisiones de la circunferencia que abarca el lado.
- Núcleo: Es el polígono que surge en su interior.
- Nodo: Cada uno de los vértices de un polígono estrellado se denomina nodo.



















No hay comentarios:
Publicar un comentario