TEMA 9: SISTEMA DIÉDRICO I. Representación del punto, la recta y el plano
El sistema diédrico es un método gráfico que se encarga de representar sobre un plano figuras o cuerpos de dos o tres dimensiones . Se trata de un conjunto de reglas o principios aplicados a dos planos perpendiculares sobre los que se proyectan los objetos (puntos, rectas, curvas o figuras).
Este método que fue mecanizado, desarrollado o estudiado en 1799 por la geometría Gaspard Monge , considerado el padre de la geometría descriptiva.
FUNDAMENTOS
El sistema diédrico tiene como base fundamental dos planos de proyección que forman cuatro ángulos rectos y cuatro cuadrantes. A estos planos los llamamos Plano Horizontal (PH) y Plano Vertical (PV) , ambos se cortan en una recta llamada Línea de tierra (LT) .
Todos los elementos (puntos, aristas, cuerpos) se representan mediante sus dos proyecciones.
Las proyecciones son Cilíndricas : todos los rayos proyectantes son paralelos entre sí.
Las proyecciones son ortogonales : los rayos proyectantes forman siempre 90º respecto a los planos de proyección.
Para poder representar el diedro en dos dimensiones, es decir sobre un plano, el plano horizontal de proyección se abate sobre el vertical, usando como charnela (eje de giro) la línea de tierra, llevando con él todas sus proyecciones de los elementos en el espacio. (Ver los dibujos de abajo).
COORDENADAS
Para situar los puntos se emplean las coordenadas . Primero estudiaremos los nombres de las distintas
coordenadas:
La lateralidad: (x) es la situación (derecha o izquierda) del punto respecto a la línea de tierra.
- Todo lo que esté situado a la derecha del punto de origen es desplazamiento positivo.
- Todo lo que esté situado a la izquierda del punto de origen es desplazamiento negativo (si se da el caso que el punto de origen no está en el margen).
El alejamiento: (y) es la distancia entre el punto y el plano vertical de proyección.
La cota: (z) es la distancia existente entre el punto y el plano horizontal de proyección (la altura).
Así, un punto siempre se sitúa de la siguiente manera P (x, y, z), o lo que es lo mismo P (lateralidad, alejamiento, cota). Por ejemplo: P(-2, 3,4).
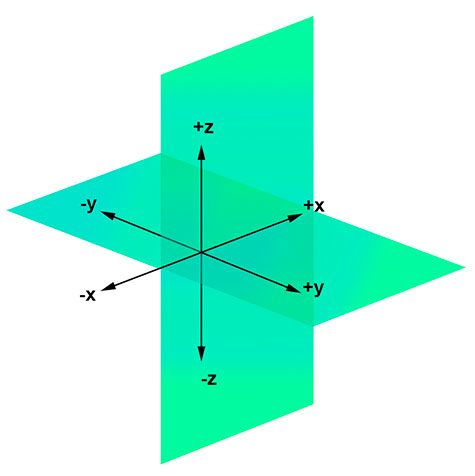
En la imagen anterior, vemos en el eje X :
- Todo lo que esté situado a la derecha del punto de origen es desplazamiento positivo .
- Todo lo que esté situado a la izquierda del punto de origen es desplazamiento negativo (si se da el caso que el punto de origen no está en el margen).
Observamos el eje Y :
- Todo lo que esté situado por delante del PV tiene alejamiento positivo .
- Todo lo que esté situado detrás del PV tiene alejamiento negativo .
Y respecto al eje Z :
- Todo lo que esté situado por encima del PH tendrá cota positiva .
- Todo lo que esté situado por debajo del PH tiene cota negativa .
NOMENCLATURAS
Para nombrar los puntos en el espacio usamos las letras mayúsculas P
Para nombrar las proyecciones las proyecciones horizontales usamos las letras minúsculas: p
Para nombrar las proyecciones verticales usando las letras minúsculas seguidas de ':p'
Nomenclatura
REPRESENTACIÓN DEL PUNTO
Un punto en sistema diédrico ortogonal se representa mediante sus proyecciones : vertical y horizontal. Las dos proyecciones siempre están alineadas en una perpendicular a la LT.
La cota es la distancia entre el punto y el plano horizontal de proyección (en proyecciones la distancia entre la proyección vertical y la LT).
El alejamiento es la distancia entre el punto y el plano vertical de proyección (en proyecciones es la distancia entre la proyección horizontal y la LT).
Aunque no es lo más habitual, algunas veces, encontramos puntos en cuadrantes diferentes al primero. En estos casos, debido al abatimiento del plano horizontal sobre el vertical, encontraremos las proyecciones verticales bajo la línea de tierra y las horizontales por encima de ella. Estos puntos a menudo los encontramos como trazas de rectas, las cuales son necesarias averiguar para poder determinar un plano.
Resumiendo: los puntos del primer diedro tienen una proyección a cada lado de LT; la horizontal por debajo y la vertical por encima.
Los puntos del segundo diedro tienen las dos proyecciones por encima de la LT; y los puntos del cuarto diedro las dos por debajo.
Los puntos del tercer diedro, como los del primero, tienen una proyección a cada lado de LT; pero la horizontal por encima y la vertical por abajo.
Alfabeto del punto
LOS BISECTOR
Son dos planos que dividen los cuadrantes en dos mitades iguales. Ambos se cortan en LT y forman 90º entre ellos, y 45º con PV y PH.
Así tenemos 8 octantes.
La primera bisectriz divide el primer y el tercer cuadrante, mientras que la segunda bisectriz divide y el cuarto cuadrante. Cualquier punto, que se encuentre en los bisectores tendrán los mismos valores de cota que de alejamiento.
En este "alfabeto" se pueden observar todos los tipos de rectas que podemos encontrar en el sistema diédrico. RECTA OBLICUA O CUALQUIERA
RECTA HORIZONTAL (paralela al plano horizontal)
RECTA FRONTAL (paralela al plano vertical)
RECTA PARALELA A LÍNEA DE TIERRA (LT)
RECTA DE PUNTA
Las rectas verticales y horizontales sólo tienen una traza sobre uno de los planos de proyección.
RECTA DE PERFIL
Arriba se encuentra la recta de perfil, la más particular de todas. Debido a su posición relativa respecto a los planos de proyección no se puede observar correctamente con solo dos vistas.
Esta circunstancia hace necesario un plano de perfil sobre el cual se proyecta una tercera vista de la recta que permita observar su inclinación respecto al plano vertical (PV) y al plano horizontal (PH).
En geometría descriptiva una recta se puede definir de dos formas:
1.- Dos puntos describen una recta.
2.- La intersección de dos planos también define una recta.
Un punto pertenece a una recta si ambas proyecciones del punto están sobre ambas proyecciones de la recta.
Las trazas de una recta son los puntos de la recta que cortan a los planos de proyección. Una recta puede tener dos trazas: la traza horizontal H (h'h), es el punto en que la recta corta el plano horizontal de proyección. La traza vertical V (vv') es el punto en que la recta corta en el plano vertical de proyección.
No todas las rectas tienen dos trazas, una recta puede tener solo una traza si es paralela a algún plano de proyección o ninguna si es paralela a ambos.
La recta horizontal, la recta frontal y la recta paralela a línea de tierra únicamente tienen una traza.
ENCONTRAR LAS TRAZAS DE UNA RECTA
Muchas veces nos encontraremos con segmentos que no se cortan con los planos de proyección, pero por necesidades del ejercicio necesitaremos encontrar las trazas de la recta a la cual pertenece el segmento.
1.- Primero prolongamos las proyecciones hasta encontrar la línea de tierra.
Las prolongaremos desde ambos extremos.
2.- Desde esos puntos de corte con la LT trazaremos perpendiculares a LT hasta que corten las otras proyecciones.
Los puntos de corte con la línea de tierra y de la perpendicular con la otra proyección son las trazas de la recta.
La línea recta está en la traza horizontal, H (h h'). Mientras que el punto de la recta con alejamiento 0 es la traza vertical de la recta, V (v,v').
Ambos puntos, como todos en diédrico, tienen dos proyecciones.
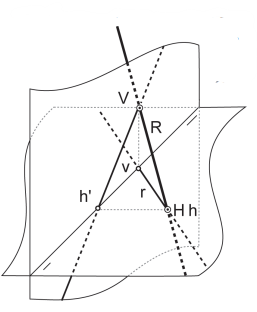
Abajo se puede observar todo esto representado en perspectiva caballera.
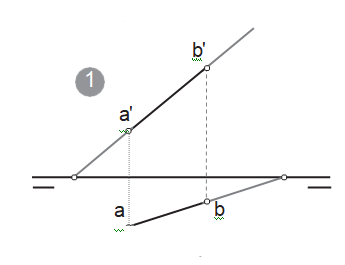
Una recta será visible siempre y cuando se encuentre en el primer cuadrante. Cuando la recta se encuentra en los demás (2º,3º y 4º) cuadrantes se representa con trazos discontinuos.
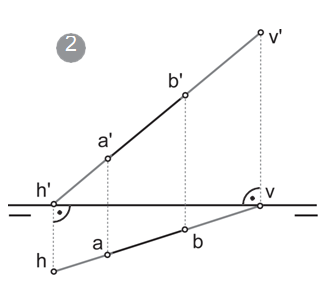
Arriba observamos una recta oblicua. Cuando la recta cruza los planos de proyección para pasar al 2º y 4º cuadrante esta queda representada por trazos discontinuos.Abajo vemos el mismo dibujo representado en sistema diédrico. Vemos como a partir de las trazas las proyecciones se representan con trazados discontinuos.
Una recta podría pasar por un solo cuadrante (este es el caso de las líneas paralelas a la LT), por dos cuadrantes (sucede con las rectas de punta vertical y de punta horizontal, horizontal o frontal) y por tres cuadrantes (cuando las rectas son oblicuas o cualquiera, también las rectas de perfil).
ESTUDIO DE VISIBILIDAD DE UNA RECTA
El estudio de visibilidad de una recta en diédrico consiste en determinar las partes de las proyecciones ocultas tras los planos de proyección (representándolas discontinuas) y las visibles (continuas) además de determinar sus trazas y de este modo por qué cuadrantes transcurre la recta.
HACER UN ESTUDIO DE VISIBILIDAD DE LA RECTA QUE CONTIENE AL SEGMENTO AB
1.- Debemos encontrar las trazas de la recta. De este modo determinamos la parte de la recta (sus proyecciones) que pasan por el primer cuadrante y las intersecciones con el plano vertical y horizontal así como también podemos representar las partes vistas y ocultas con trazos continuos o discontinuos.
Con este primer paso podemos estar seguros de que el segmento H (hh') V(vv') se encuentran en el primer cuadrante.
2.- A partir de aquí debemos determinar por qué otros cuadrantes pasan la recta cuando cruza los planos de proyección.
1.- A la izquierda de hh' la proyección vertical de la recta se encuentra bajo la LT por lo tanto las cotas en esta parte de la recta son negativas, mientras la proyección horizontal se mantiene también bajo la LT. Esto implica: Cotas negativas y alejamientos positivos = 4º Cuadrante
2.- A la derecha de vv' la proyección vertical se mantiene sobre la LT lo cual significa que las cotas son positivas mientras la proyección horizontal de la recta se sitúa sobre LT por lo que los alejamientos en este caso son negativos. Concluyendo de nuevo: Cotas positivas y alejamientos negativos = 2º Cuadrante
3.- Los puntos aa' y xx' son puntos donde el valor absoluto (el número, sin signo) es igual por lo que son puntos donde la recta atraviesa los planos bisectores. aa': cota positiva, alejamiento positivo = corta el primer bisector. xx': cota negativa, alejamiento positivo = corta al segundo bisectriz.
TERCERA PROYECCIÓN DE UN PUNTO
Si bien en sistema diédrico contamos con la proyección vertical y la proyección horizontal como las vistas principales y necesarias del sistema, en algunos casos podemos necesitar observar los elementos (principalmente rectos y planos) en una tercera proyección auxiliar .
En primer lugar vamos a estudiar la tercera proyección con un punto genérico en el 1er cuadrante:
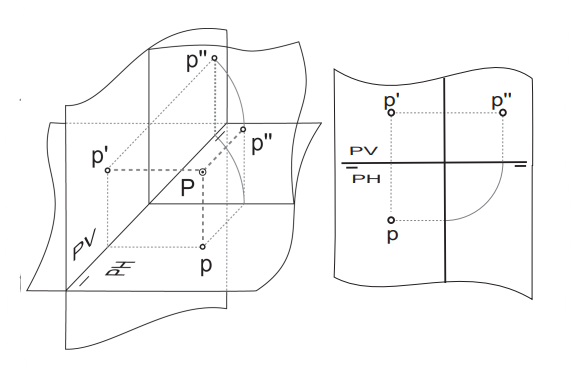
La operación consiste en trazar un plano de perfil , podemos hacerlo en la lateralidad que más nos convenga, a la izquierda oa la derecha En la p'p''.
En la mayoría de los casos nos conviene apartarlo para poder tener la zona de las proyecciones horizontal y vertical despejada.
1- Una vez hemos trazado el plano de perfil proyectamos sobre este, ortogonalmente, el punto (este quedará a la misma cota).
2- Para hacerlo debemos proyectar sobre el plano de perfil la proyección horizontal y la vertical .
Finalmente
abatimos el P. de perfil sobre el PH de proyección empleando como charnela(eje de giro) la traza vertical del plano de perfil.
yo La mecánica siempre es la misma. Hay que andarse con ojo cuando el punto a proyectar en tercera proyección cambia de cuadrante, pues aunque el método no cambia si que cambia la disposición y el sentido del abatimiento. Veamos abajo que sucede cuando hacemos la tercera proyección de un punto en el tercer cuadrante.
Como se observa, el arco que representa el abatimiento del plano de perfil, en este caso se encuentra sobre la línea de tierra ya la izquierda del plano de perfil. Esto se debe a que el abatimiento siempre afecta al alejamiento y no a la cota que permanece al ser el abatimiento del plano de perfil sobre el plano Vertical de proyección.
Como se observa en ambos puntos (1er Cuadrante arriba y 3er Cuadrante a la izquierda) las trazas de plano de perfil auxiliar ayudan a ver el punto como si estuviéramos observando el sistema propiamente dicho, de perfil.
Para observar una recta en tercera proyección debemos de llevar a la tercera proyección dos puntos pertenecientes a esta.
En realidad las únicas rectas que, en sí mismas, necesitan de una tercera proyección en el sistema diédrico son las rectas de perfil, que por su naturaleza no se pueden observar bien en las dos proyecciones más convencionales (PH y PV).
1.- Trazamos el plano de perfil auxiliar, proyectamos los dos puntos en él y lo abatimos sobre el vertical, de este modo ya observamos las terceras proyecciones de ambos puntos.
2.- Trazamos la recta r", así podemos observar su inclinación respecto a ambos planos de proyección e incluso observar sus trazas verticales y horizontales que podemos llevar a las dos proyecciones corrientes.
Debajo observamos como se ha llevado a cabo el mismo procedimiento de las ilustraciones arriba de estas líneas, pero en este caso trazando el plano auxiliar de perfil de modo que contiene a la propia recta de perfil, esto puede ahorrar espacio y en algunos casos es aconsejable, pero en muchos otros, la mayoría de los problemas, suele ser más indicado trazar la tercera proyección a un lado para que no se confunda con el resto del problema.
Un plano se representa mediante sus trazas. Las trazas de un plano son las rectas de intersección del plano con los planos de proyección.
Mientras al punto en el espacio le dábamos nombre con una letra mayúscula ya sus proyecciones con la minúscula y minúscula prima A (a a'), a un plano lo nombraremos siempre con mayúsculas P (PP').
En este "alfabeto" se pueden observar todos los tipos de plano que podemos encontrar en el sistema diédrico. Todos están representados en perspectiva caballera (izquierda) y junto a ella la representación en diédrico (derecha).
Abajo se puede observar un plano de perfil cuyas trazas forman una línea perpendicular a LT. Este tipo de plano es muy útil para representar puntos, rectas, planos y cuerpos con una tercera proyección.
Abajo dos planos: "paralelo a LT" y que "contiene LT"
Debido a su posición relativa respecto a los planos de proyección no se puede observar, u operar con ellos, correctamente con solo dos proyecciones.
Esta circunstancia hace necesario un plano de perfil sobre el cual se corta proporcionando una tercera vista del plano que permita observar su inclinación respecto al PV y el PH.
Los planos que contienen a la LT se representan con un punto de contenido en él, un trazo a cada lado de la línea de referencia que una de las proyecciones.
Estos planos también son muy susceptibles de ser representados en tercera proyección.
En geometría descriptiva un plano puede ser definido por distintos datos:
1.- Tres puntos no alineados. (Tres puntos describen un triángulo y cualquier polígono, todo polígono está siempre contenido en un solo plano).
2.- Una recta y un punto no perteneciente a ella.
3.- Dos rectas que se cortan.
4.- Dos rectas paralelas.
Otras nociones a tener en cuenta:
Un punto pertenece a un plano cuando podemos contenerlo en una recta perteneciente al plano.
Una recta pertenece a un plano si sus trazas (que son dos puntos) están contenidas en las trazas del plano (que son dos rectas).
Normalmente, para dibujar un plano a partir de otros datos habrá que buscar dos rectas y sus trazas.
Caso 1: Tres puntos no alineados definen un plano:
Necesitaremos al menos tres de las cuatro trazas de dos rectas que pasen por dos de los tres puntos.
Trazar el plano que contiene a los puntos a, por c.
1.- Trazamos las proyecciones de la recta ac y hallamos sus trazas hy v. 2.- Trazamos las proyecciones de la recta cb y hallamos sus trazas hy v.
3.- Unimos las h (trazas horizontales) de ambas rectas y las v (trazas verticales).
Caso 2 y 3: Una recta y un punto no perteneciente a esta o dos rectas que se cortan.
Se trata en realidad del mismo caso que el primero ya que podemos elegir dos puntos pertenecientes a la recta que delimitan el tercer segmento de un triángulo cuyos vértices son estos dos extremos del segmento y el otro punto no perteneciente a la recta.
Dibujar las trazas del plano que contiene al punto aya la recta r.
1.- Hallamos las trazas de la recta r. Por h pasará la traza horizontal del plano y por v' la vertical.
2.- Elegimos un punto bb' sobre ry trazamos una recta(s) que pasa por ay por b. Hallamos las trazas de s.
3.- De las rectas rys debemos al menos haber obtenido tres de sus trazas (dos horizontales y una vertical y viceversa) de este modo ya podremos trazar las trazas del plano buscado ya que sabemos que la intersección de la línea de tierra con cualquier traza de un plano es también un punto perteneciente a la otra traza.
- En el caso de que con los pasos 2 y 3 no hubiéramos encontrado las trazas de rectas suficientes para situar las del plano elegiremos más puntos pertenecientes ary trazaremos más rectas desde el punto a por esos puntos para obtener nuevas trazas de rectas pertenecientes al plano.
Caso 4: Dos rectas paralelas definen un plano
Se trata en realidad del mismo caso que el primero ya que podemos elegir dos puntos pertenecientes a la recta que delimitan al tercer segmento de un triángulo cuyos vértices son estos dos extremos del segmento y el otro punto no perteneciente a la recta.
Trazar las trazas del plano que contiene a las rectas rys
1.- Hallamos las trazas de la recta r. 2.- Hallamos las trazas de la recta s.
3.- Unimos las h (trazas horizontales) de ambas rectas y las v (trazas verticales).
Trazar las trazas del plano que contiene a las rectas ry s. En este caso ambas rectas son paralelas a LT.
1.- Trazamos un plano de perfil que corta a todas las proyecciones de ambas rectas. Abatiendo este y sus intersecciones con las dos rectas podremos visualizar intersecciones con las dos rectas podremos visualizar mejor el plano que buscamos.
2.- Representamos las rectas sobre el plano de perfil abatido, esta tercera proyección serán los puntos (r) y (s).
3.- Trazamos la recta que une (r) con (s) esta representa al plano buscado de perfil. El punto (v) representa su traza vertical y el punto (h) la horizontal.
4.- Por (v) trazamos una recta horizontal que será la traza horizontal desabatida. Llevamos la distancia del alejamiento de (h) sobre el plano de perfil inicial ya partir de esta distancia trazamos una horizontal que será la traza horizontal desabatida.

La mayoría de problemas en sistema diédrico requieren contener rectas en planos, hacer pasar rectas por puntos o planos por puntos.
Si necesitamos contener una recta en un plano o un punto en un plano los planos proyectantes nos sirven para este fin de manera rápida y limpia.
Trazar un plano proyectante vertical u horizontal por una recta cualquiera
Los planos proyectantes reciben dicha denominación porque todo lo que contienen queda proyectado en la traza proyectante. Por ejemplo: todos los puntos, rectas y figuras planas contenidas en un plano proyectante vertical se proyectarán
sobre su traza vertical, la otra traza es siempre perpendicular a la LT.
Dicho esto, es sencillo trazar planos proyectantes que contengan a rectas oblicuas haciendo coincidir una de las
proyecciones de la recta con la traza homónima del plano.
CONTENER RECTAS HORIZONTALES Y FRONTALES EN PLANOS
La mayoría de problemas en sistema diédrico requieren contender rectas en planos, hacen pasar rectas por puntos o planos por puntos.
Si necesitamos contener una recta en un plano el tipo de recta idónea para ello son las rectas horizontales y las frontales. Estas en la mayoría de ocasiones sirven para nuestros propósitos dentro del problema y se contienen en los planos de forma limpia y rápida.
Contener una recta horizontal en un plano oblicuo
1.-Trazamos la proyección vertical de la recta R, r’,(si nos piden alguna cota particular lo haremos a esa distancia
de LT). Esta proyección en este tipo de recta es siempre paralela a LT,
horizontal.
2.-En la intersección de r' con P' se encuentra v' (traza vertical de la recta R) trazamos por v' una perpendicular a
LT hasta cortarla, en esta intersección se encuentra v (proyección horizontal
de la traza vertical de la recta R).
3.-Por v trazamos una paralela a P (traza horizontal del plano).
Contener una recta frontal en un plano oblicuo
1.-Trazamos la proyección horizontal a de la recta R, r,(si nos piden algún alejamiento particular lo haremos a esa
distancia de LT). Esta proyección en este tipo de recta es siempre paralela a
LT, horizontal.
2.-En la intersección de r con P se encuentra h (proyección horizontal de la traza horizontal de la recta), trazamos
por h una perpendicular a LT hasta cortarla, en esta intersección se encuentra
h' (proyección vertical de la traza horizontal de la recta R).
3.-Por h' trazamos una paralela a P' (traza vertical del plano).
APLICACIONES O PROBLEMAS BÁSICOS
Hallar la proyección horizontal del punto A, del cual conocemos su proyección vertical a',
perteneciente al plano P.
1.- Trazamos una recta horizontal cuya traza vertical pasa por a'.
2.- Trazamos una perpendicular a LT por a', donde esta corta a la proyección horizontal de la recta encontramos a.
Hallar la traza vertical P' del plano P, del cual conocemos su traza horizontal P y que contiene al
punto A (a',a)
1.- Trazamos una recta frontal cuya traza horizontal pasa por a. A partir de h' (proyección vertical de la traza horizontal de la recta) trazamos la proyección vertical de la recta por a'.
2.- Trazamos una paralela a la proyección vertical de la recta a partir de la intersección de la traza horizontal del plano con LT.
POLÍGONOS CONTENIDOS EN PLANOS
Para que un polígono este
contenido en un plano todos sus vértices deberán estar contenidos en elplano.
Para demostrar o comprobar que un polígono pertenece en su totalidad a un plano necesitamos
pasar por los vértices del polígono rectas contenidas en el plano, eso es
sencillo si empleamos rectas horizontales o frontales.
Un ejercicio básico muy común es:
1.- Por uno de los vértices del polígono trazamos una recta frontal contenida en el plano (en este ejercicio hemos usado una recta frontal, pero esto es lo mismo que si hubiéramos pasado por el punto una horizontal). Llevamos el punto a la proyección horizontal.
2.- Repetimos la operación con el resto de vértices. Una vez llevados a proyección horizontal todos los vértices ya podemos trazar la proyección del polígono completo.
Otra opción igualmente válida para resolver este problema sería prolongar los segmentos que forman el polígono dado hasta cortar a la traza vertical del plano P' y a la LT. Esto nos permite determinar ambas trazas de la recta que contiene al lado del polígono y por lo tanto determinar la proyección horizontal de la misma y así la proyección horizontal del polígono. Pero esto en ocasiones puede resultar imposible al encontrarse las trazadas de dichas rectas fuera del papel.
Dada la proyección vertical de un polígono y las trazas del plano paralelo a LT al que pertenece
hallar la proyección horizontal del polígono.
En el paso 1 hemos trazado la tercera proyección
de P. En el segundo paso hemos llevado el polígono al plano en tercera proyección y hemos llevado el alejamiento a la proyección horizontal. A la derecha vemos el mismo resultado
pero conteniendo los lados en rectas, trazando las proyecciones horizontales de
esta y bajando los puntos sobre estas.
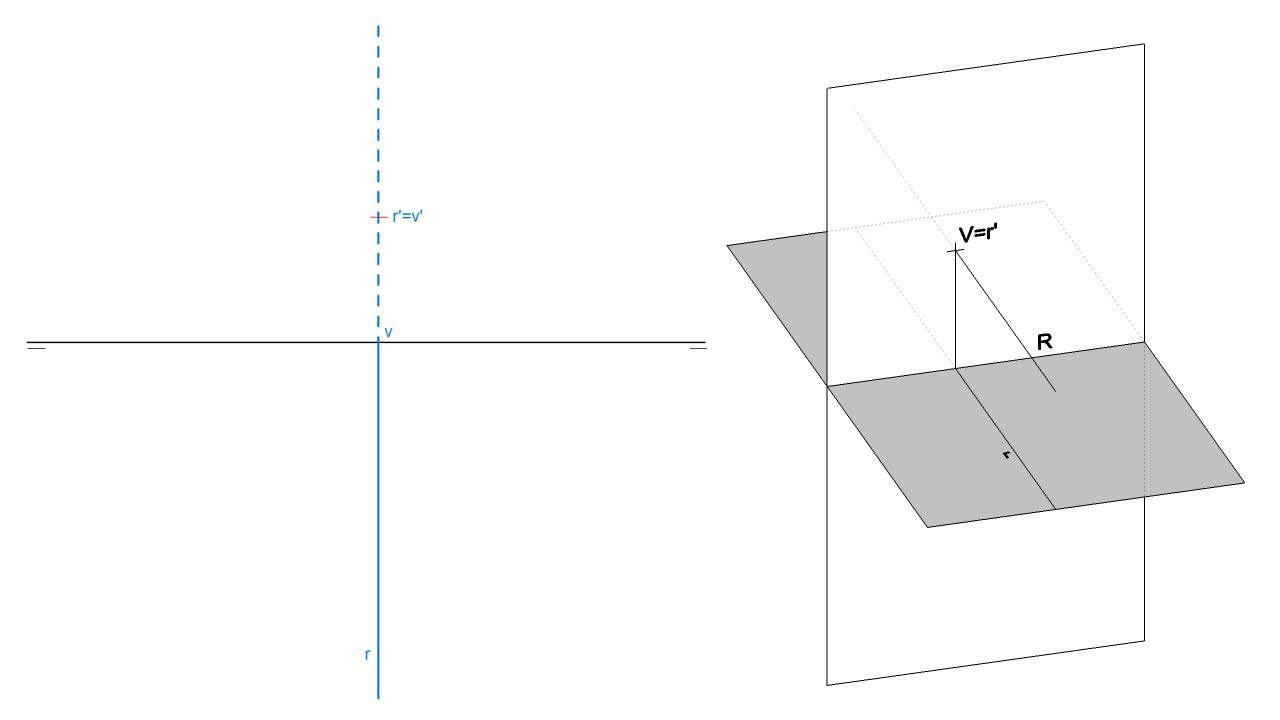
Recta de máxima pendiente (LMP) de un plano
Es una recta perteneciente al plano que forma el máximo ángulo posible con PH. En este caso la recta es perpendicular a la traza horizontal del plano. Un plano tiene infinitas rectas de máxima pendiente.
Recta de máxima inclinación (LMI) de un plano
Es una recta perteneciente al plano que forma el máximo ángulo posible con el PV. En este caso la recta es perpendicular a la traza vertical del plano. Un plano tiene infinitas rectas de máxima inclinación.















































No hay comentarios:
Publicar un comentario