TEMA 10: PERSPECTIVA AXONOMÉTRICA ORTOGONAL
AXONOMÉTRICA: Axo (Ejes) + Métrica (medidas).Axonométricas son todas aquellas representaciones
de objetos o figuras que se han llevado a cabo a partir de tres ejes.
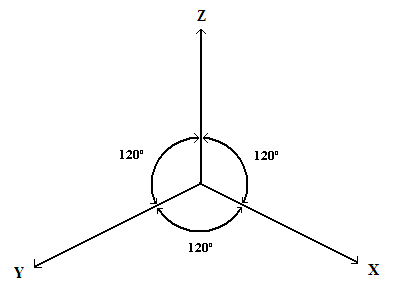
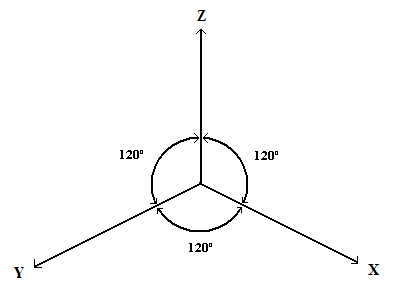
El Sistema Axonométrico está formado por tres ejes (x, y, z). Hay tres tipos de axonométricos: el trimétrico que tiene los tres ángulos desiguales, el dimétrico que tiene dos ángulos iguales y el isométrico que tiene tres ángulos iguales.
ELEMENTOS
TRIEDRO TRIRECTÁNGULO: Triedro (tres
planos) + Trirectángulo (tres ángulos rectos). Si a un cubo le
suprimimos tres de sus planos nos quedamos con tres planos que forman ángulos rectos dos a dos. Estos
tres planos producen tres rectas intersección que serán los ejes de coordenadas
(x, y, z). El punto en común de las tres rectas es el origen de coordenadas.
PLANO DEL CUADRO: También llamado plano de referencia es aquel donde proyectan los tres ejes producido por el triedro. Es el equivalente a una pantalla de cine, un cristal donde se calca la realidad tridimensional o el papel donde dibujamos.
PROYECCIONES: La proyección de un punto es la intersección de una recta proyectante en un plano (otro
punto) pasando la recta por dicho punto. La proyección de una recta es el
conjunto de intersecciones de rectas proyectantes (infinitas, aunque con dos
bastan para definir una recta) en un plano, pasando todas las rectas
proyectantes por dicha recta.
TIPOS DE PROYECCIONES: Cuando las rectas proyectantes son paralelas en el espacio se dice que estamos ante una proyección cilíndrica. Cuando las rectas proyectantes parten todas de un mismo punto o foco se dice que estamos ante una proyección cónica. Las proyecciones en axonométrica son cilíndricas.
TIPOS DE PROYECCIONES ENAXONOMÉTRICA
Para obtener los ejes axonométricos, o triedro de coordenadas proyectaremos el triedro trirectángulo sobre
el plano de cuadro. Las proyecciones son siempre cilíndricas. Pero estas
respecto al plano de cuadro pueden ser ORTOGONALES (las rectas proyectantes
forman 90º respecto al plano de proyección) u OBLICUAS (las rectas proyectantes
forman un ángulo distinto a 90º respecto al cuadro).
AXONOMÉTRICAS ORTOGONALES:
Dependiendo de la posición relativa del triedro trirectángulo respecto al plano de cuadro, las proyecciones ortogonales producirán unas magnitudes angulares entre los ejes diferentes.
Si los ejes se proyectan sobre el cuadro formando (120º) nos encontramos ante una perspectiva ISOMÉTRICA, si dos ángulos son iguales la perspectiva será DIMÉTRICA y si cada ángulo tiene una magnitud diferente se tratará de una TRIMÉTRICA.
Del mismo modo la posición relativa del triedro respecto al plano de proyección provocará que los ejes sufran una reducción en sus magnitudes.
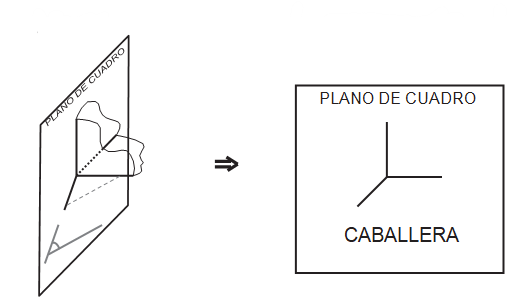
AXONOMÉTRICA OBLICUA- CABALLERA:
En este caso uno de los planos del triedro trirectángulo coincide con el plano del cuadro. Las proyecciones ortogonales proyectarían en el tercer eje de coordenadas en un solo punto. Esto se resuelve proyectando respecto al plano de proyección. De este modo este será el único eje que se vea sometido a una reducción.
REDUCCIÓN: Una reducción es una disminución de la verdadera magnitud de un segmento provocada por una proyección cuando una recta no es paralela al plano de proyección. El coeficiente de reducción se expresa mediante una fracción o mediante un número con decimales (menor que uno).
Esto mismo les sucede a los ejes del sistema axonométrico ortogonal ya que estos nunca son paralelos al plano del cuadro. En perspectiva isométrica los tres ejes se ven siempre sometidos a la misma reducción (0,816). En dimétrica el eje que divide los dos ángulos iguales se ve sometido a una reducción mientras que los otros dos, los que forman el ángulo desigual, están marcados por otra misma reducción. Y en trimétrica cada eje se somete a un coeficiente de reducción distinto.
El triángulo de trazas es la intersección producida en el triedro trirectángulo por un plano paralelo al plano
de cuadro.
En el triedro de coordenadas (proyectado en el plano de cuadro) este tiene los lados siempre perpendiculares al eje de coordenadas opuesto.
En el triedro trirectángulo no solo son perpendiculares entre sí los planos, sino que también lo son sus intersecciones (los ejes axonométricos).
Sin embargo en proyecciones estas magnitudes angulares se ven alteradas. En isométrica encontramos tres ángulos iguales de 120º, en dimétrica los 360º de la circunferencia son divididos en tres porciones, una de ellas desigual y en trimétrica encontramos tres magnitudes angulares diferentes.
El triángulo de trazas sirve para abatir sobre el plano auxiliar que lo produce estos ángulos desvirtuados, contenidos
en los planos de coordenadas, utilizando como charnela o eje de giro sus lados.
De este modo situamos los planos de coordenadas en una posición frontal al cuadro para observar esas porciones
de los ejes y los ángulos que estos producen en verdadera magnitud.
Es importante la dirección de afinidad, siempre perpendicular a los lados del triángulo de trazas que es el eje de afinidad
(lo cual es lo mismo que una prolongación de
los ejes), esta nos permitirá llevar las medidas y las formas desde los ejes
abatidos hasta la perspectiva axonométrica.
En conclusión, el triángulo de trazas sirve para aplicar el coeficiente de reducción del sistema isométrico de una manera gráfica.
Coeficiente de reducción y triángulo fundamental de trazas
Construcción del triángulo de trazas:
Ejes (x, y, z)
Abatimiento del plano horizontal
1.- Alargamos el eje z en discontinuo
2.- Trazamos una perpendicular al eje z.
3.- Buscamos punto medio de la perpendicular
4.- Hago un arco capaz de 90º
5.- Surge el punto o del alargamiento y el corte con el arco capaz (o) en verdadera magnitud.
Abatimiento del plano frontal
1.- Alargamos el eje en discontinuo
2.- Trazamos una perpendicular al eje y
3.- Buscamos el punto medio de la perpendicular
4.- Hago arco capaz de 90º
5.- Surge el punto o del alargamiento y el corte con el arco capaz (o) en verdadera magnitud.
Abatimiento del plano de perfil
1.- Alargamos el eje x en discontinuo
2.- Trazamos una perpendicular al eje x
3.- Buscamos punto medio de la perpendicular
4.- Hago arco capaz de 90º
5.- Surge el punto o del alargamiento y el corte con el arco capaz en verdadera magnitud.
Triángulo fundamental de trazas
NOTA: Para el Sistema Dimétrico y Trimétrico se haría de igual forma pero utilizando la mediatriz para encontrar el punto medio del arco capaz.
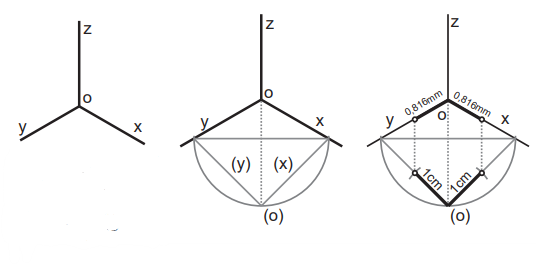
ISOMÉTRICA: Los ejes en la perspectiva isométrica forman tres ángulos iguales de 120º. Y en relación con esto los tres ejes se ven sometidos a una misma reducción cuando se proyectan sobre el plano de cuadro o referencia.
En perspectiva isométrica no es necesario abatir las tres porciones del triedro para observar sus ejes en verdadera magnitud y forma, pues los tres son iguales. Bastará simplemente con trazar un solo lado del triángulo de trazas y abatir un solo plano de coordenadas. Es más al ser todas las perspectivas isométricas iguales no necesitaremos realizar esta operación conociendo que el coeficiente de reducción de todos sus ejes es 0,816.
Nos quedaría por abatir y aplicar la afinidad al eje z, lo cual no es necesario, pues sabemos que en este sistema axonométrico los tres ejes sufren la misma reducción.
Conociendo esta reducción tampoco es necesaria esta operación que hemos aplicado aquí para demostrar el coeficiente de 0,816.

Arriba observamos un método para realizar una escala gráfica Isométrica que es derivada de la afinidad anterior.
Le aplicas una medida al ángulo de 45º y bajando esa medida en vertical al ángulo de 30º se queda reducida.
Aunque en la mayoría de los casos, cuando se realiza una perspectiva isométrica no se aplican los coeficientes de reducción a los ejes. Ya que , al contar estos con la misma reducción , la diferencia entre aplicar coeficientes y no aplicarlos tan solo causa una pequeña variación de escala del dibujo resultante, siendo de un modo u otro una figura semejante el dibujo final. Cuando la perspectiva isométrica no tiene aplicadas las escalas de los ejes o coeficientes de reducción suele referirse a ella como "dibujo isométrico". Aunque también puede especificar "perspectiva isométrica sin aplicar los coeficientes de reducción".
En el dibujo isométrico el coeficiente es uno, así que se quedaría igual.
Si miras el alzado por el lado derecho, el perfil lo miras por el lado izquierdo. Cuando es un perfil izquierdo se sitúa a la derecha del alzado.
Trazado de la circunferencia en el sistema isométrico
La representación de una circunferencia en el sistema isométrico es una elipse. Sin embargo, en el denominado dibujo isométrico se admite el óvalo inscrito en un rombo, figura en la que se transforma el cuadrado circunscrito a la circunferencia como sustituto de la elipse isométrica.
La Escala
Escala final = 2/3 = 8/9 =0,88 = a todas las medidas de la figura le tienes que multiplicar por esta cifra.
Escala inicial 3/4
(2x4 3x3)
Si fuera perspectiva isométrica habría que multiplicar también por el coeficiente.
El coeficiente se aplica para que la figura parezca más realista.
x 0,816 : 0,816
E = E.F. = 2/3 = 2/3 =0,66 (El número de arriba de la fracción de la escala es más pequeño que el de abajo, se trata de una
E.I. 1/1 escala de reducción).
i x E =f -- E= f/i = 2/3 / 1/1 = 2/3












No hay comentarios:
Publicar un comentario